Michal Kwasigroch

Dr Michal Kwasigroch
Director of Studies in Maths with Physics and Natural Sciences
College Temporary Lecturer
Research Fellow at UCL
Member of Trinity College
Visitor in Prof Castelnovo's group
Office: 506 Mott Bld
Phone: +44(0)1223 3 37476
Email: mpk32 @ cam.ac.uk
TCM Group, Cavendish Laboratory
19 JJ Thomson Avenue,
Cambridge, CB3 0HE UK.
Research & Teaching
Research
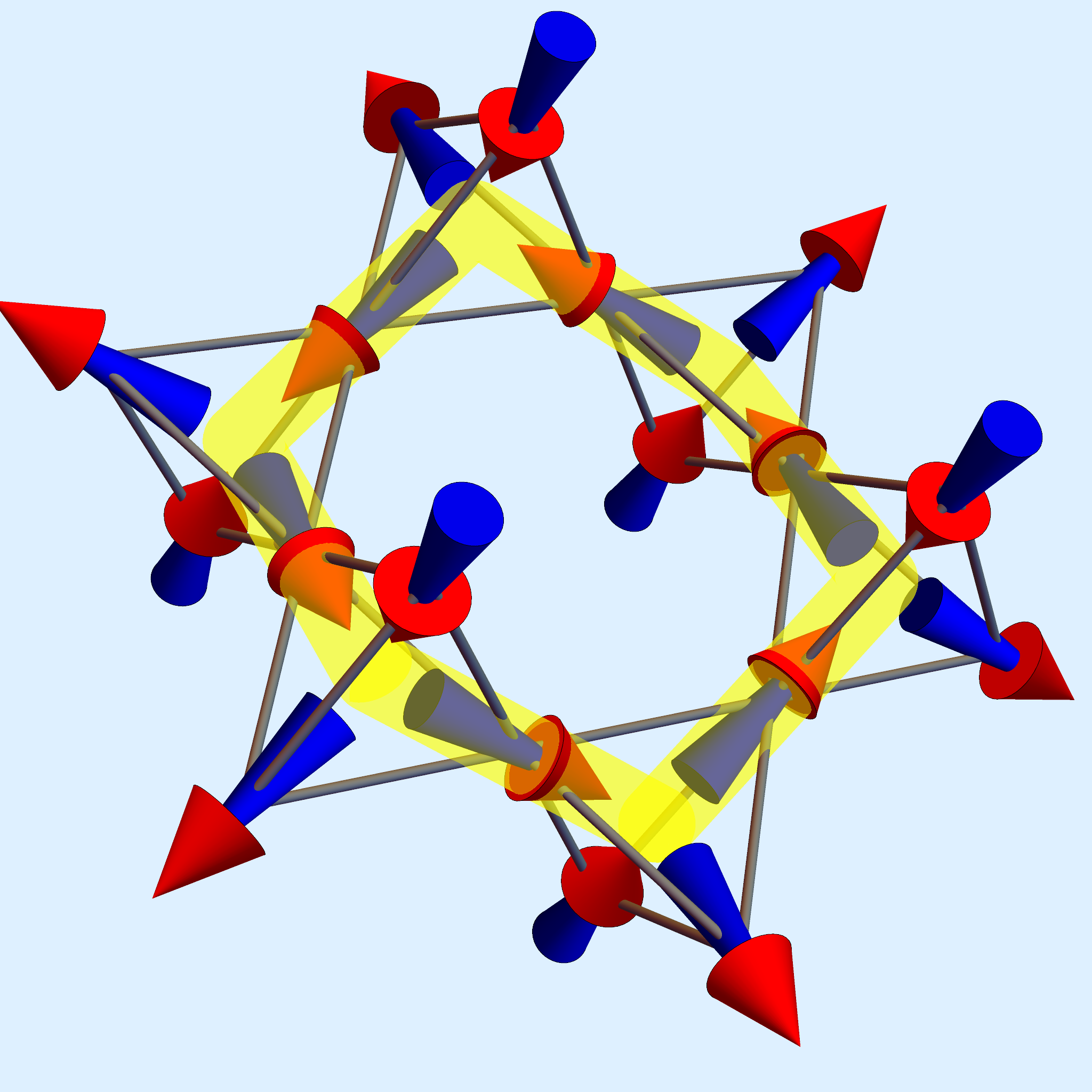
I study strongly-fluctuating condensed matter. I am particularly interested in systems, where fluctuations give rise to new and exotic phases. Examples include quantum spin liquids (QSL), many-body localised states (MBL) and the Kondo insulator. In QSLs, strong fluctuations induced by local constraints prevent magnetic moments from ordering down to absolute zero. A particularly exciting example is quantum spin ice (see picture on the left), a purported state of matter in some rare-Earth pyrochlores. It is described by a lattice version of Maxwell's theory of light and harbours topological excitations such as magnetic monopoles and fictitious electric charges. Other strongly-fluctuating systems which I have studied include ultracold polar molecules subject to strong disorder, which localises the interacting excitations of the sytem (many-body localisation) and stops it from thermalising. More recently, I have been looking at how fluctuations of magnetic moments induced by scattering with conduction electrons (Kondo effect) allow the moments to align along the hard-axis, i.e. against the forces from the crystal (see below).
Teaching
Have a look at an online demonstration of a typical Cambridge supervisionMSci and summer projects offered
- Thermal Confinement of Magnetic Monopoles
- Meissner effect in quantum spin ice
- The ferromagnetic quantum critical point
Part III Phase Transitions (Lecturer and course leader)
- Statistical Field Theory
- Quantum Field Theory
- Renormalisation Group Theory
- Universality
IA Mathematics for Natural Sciences
- Scientific Computing (Head of Class)
- Vector Calculus (Supervisor)
- Elementary Analysis (Supervisor)
- Linear Algebra (Supervisor)
- ODEs (Supervisor)
- PDEs (Supervisor)
- Probability and Statistics (Supervisor)
- Fourier series (Supervisor)
IB Physics (Supervisor)
- Oscillations Waves and Optics
- Quantum Mechanics
- Condensed Matter
- Electromagnetism
- Classical Dynamics (incl fluids)
- Thermodynamics and Statistical Mechanics
IA Physics (Supervisor)
- Waves and Optics
- Quantum Mechanics
- Special Relativity
- Rotational Mechanics
- Fields
- Dynamics

In Plain English
Fluctuations can allow the seemingly impossible to happen. Nature
abounds with examples of such phenomena. A prominent and commonplace
example is the pendulum, which remains stable in the inverted position
if the support is ever so slightly fluctuating. A more esoteric
instance is the attraction of two metal plates in totally empty space
because of the omnipresent and small quantum fluctuations of
electromagnetic fields. A theme that emerges from the above is the
subtle, all too-easily-missed role of fluctuations, with profound and
counterintuitive consequences.
Fluctuations have a huge influence
on the state of matter. They can even become infinitely strong if the
external conditions are just right. Such conditions are known as
quantum critical points and describe an amazing fractal state where
infinite fluctuations give birth to novel forms of matter. This is why
quantum critical points are the matter analogue of stem cells. These
new forms of matter include novel and unusual superconductors. Much
research has been devoted to superconductivity, in particular since
the discovery of high-temperature superconductors in the 1980s. The
quest for a room temperature superconductor is spurred by the huge
technological advances that would follow such as lossless conduction
of electricity or magnetically levitating trains. It is therefore no
wonder that much effort has been put into searching for novel
superconductors in the vicinity of quantum critical points in the hope
that these would be robust against higher temperatures.
The
places to look for new Physics are therefore those where fluctuations
are strong. Particularly perplexing is the recent discovery of exotic
magnetism in at least 12 very different compounds. The materials
contain little magnets that can align with each other. The direction
of this alignment suddenly flips just when the material is about to
become magnetic at low temperatures. My research tries to figure out
what can be responsible for this sudden re-orientation of the little
magnets.
Even though the compounds are all different they all
have large magnetic fluctuations and some even have quantum critical
points. The fluctuations are of a particular origin and are caused by
electrons that conduct electricity and which collide with the little
magnets. This is why their effect also shows up in the highly unusual
reduction of the material’s resistance to electric current when it is
heated up. My research tries to understand how these fluctuations can
cause a sudden flip in the alignment of the little magnets.
Amazingly, so far it appears that these fluctuations allow the little
magnets to line up against the forces coming from the material’s
crystal structure. This is a bit like a fluctuating pendulum lining up
against gravity. Even more amazingly, conduction electrons and little
magnets become entangled and they can be in more than one state at the
same time, like Schrodinger’s cat which is simultaneously dead and
alive. On top of this, what each one actually does, depends on the
state of the other. Such entanglement is also behind the infinite
fluctuations of quantum critical points, so there is an exciting
prospect for my research to explore how the fluctuations that flip
alignment of the little magnets can give rise to new and exotic forms
of matter such as superconductivity.
Featured Publications
- Synchronization transition in dipole-coupled two-level systems with positional disorder Phys. Rev. A 96 053610 (2017)
- Semiclassical approach to quantum spin ice Phys. Rev. B 95 (2017)
- Bose-Einstein condensation and many-body localization of rotational excitations of polar molecules following a microwave pulse Phys. Rev. A 90 021605 (2014)
- Quantum fluctuations of vortex lattices in ultracold gases Phys. Rev. A 86 063618 (2012)