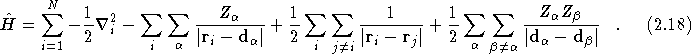
The Variational quantum Monte Carlo (VMC) method is the simpler of the two quantum Monte Carlo methods used in this thesis. It is based on a combination of the ideas described in the two previous sections, namely the variational principle and Monte Carlo evaluation of integrals using importance sampling based on the Metropolis algorithm.
Within the Born-Oppenheimer approximation [4], the Hamiltonian for a many body system can be written as
The expectation value of the exact groundstate wavefunction, 
,
with this Hamiltonian, is the exact groundstate energy.
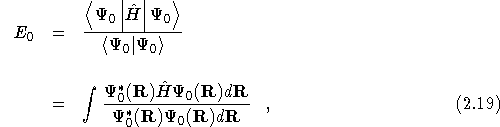
where 
denotes the 3N-dimensional vector of electronic positions.
The VMC method relies on one being able to construct a trial
wavefunction, 
, that is a reasonably good approximation to the
true groundstate wavefunction, . The subject of how to
produce a good trial wavefunctions is dealt with in depth in
chapter 
. The energy associated with the trial
wavefunction is given by,
The variational principle, described in
section , ensures that the energy, 
,
is a rigorous upper bound to the true groundstate energy, 
.
The VMC method is a Monte Carlo method for evaluating the
multi-dimensional integral in Eq.(). This is achieved by
rewriting Eq.() in the following form,
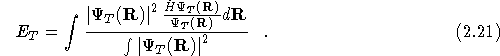
The Metropolis algorithm is used to sample a series of points,
, in configuration space. At each of these points the
``Local Energy'', 
, is
evaluated. After a sufficient number of evaluations of the local
energy have been made, the average is taken in the same way as in
Eq.().
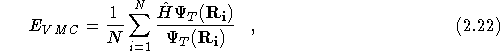
where the Metropolis algorithm ensures that in the limit of large N,
the 
are sampled from 
.
Figure: Flow chart illustrating the VMC algorithm.
Figure is a schematic flow chart illustrating how a
typical VMC algorithm works. There are two distinct parts to the
algorithm; an initial equilibration stage and an energy evaluation
stage. During the initial equilibration stage, the walker is moved
according to the Metropolis algorithm, but the local energy is not
accumulated along the walk. This stage is required because the
initial starting point of the walker is chosen randomly and therefore
a set of Metropolis moves are required before the average along its
walk is correctly sampling the distribution, 
. The
required number of equilibration steps can be established by
calculating the energy at each step from the beginning of the random
walk and looking for the point at which there is no longer a drift in
the average value of the local energy. During the energy evaluation
stage, the energy of the walker is accumulated after each move. The
method of evaluating the local energy within the QMC code is described
in more detail in section . The method of
updating the value of the wavefunction after each move is describing
in appendix .
