), but the real strength of this
principle lies in finding ground state energies. If a trial function,
, is guessed for the ground state then the expectation value
of the Hamiltonian is
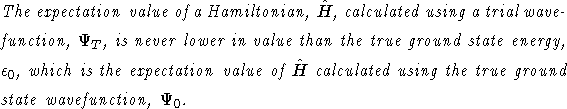
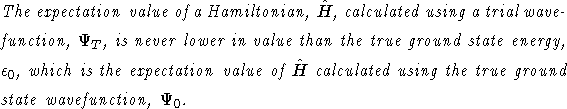
The true normalized eigenfunctions, 
, of 
form a
complete basis, so the trial wavefunction, , may be expanded
as a linear combination of these eigenfunctions,
with
As the are normalised it follows that is
normalised. Using the expansion of to calculate
from Eq.() gives
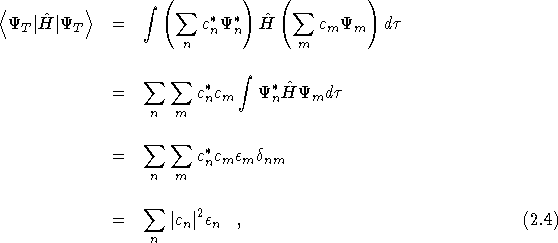
where 
is the eigenvalue corresponding to eigenstate
. Since 
for all n, it is clear
that
Variational calculations rely on making a physically plausible guess
at the form of the ground state wavefunction, , of the
Hamiltonian, . This guess will be referred to as the
trial/guiding wavefunction throughout this thesis. The ``trial'' part
of the name refers to the use of the wavefunction as a guess of the
true groundstate wavefunction to be used as the input wavefunction in
a Variational quantum Monte Carlo (VMC) calculation. The ``guiding''
part refers to the use of the same wavefunction as an input
wavefunction in the Diffusion quantum Monte Carlo (DMC) algorithm as
part of the mechanism to introduce importance sampling. This will
described in more detail in section . The
trial/guiding wavefunction depends on a number of variable parameters
which can be adjusted to minimise the energy expectation value. If the
guessed values of these parameters are good and the chosen functional
form builds in enough variational freedom to adequately describe the
physics of the system being studied, then very accurate estimates of
the ground state energy can be obtained. Variational quantum Monte
Carlo (VMC) calculations are direct applications of the above
variational principle.
