The single-particle kinetic energy operator for electron i is
The expected kinetic energy of electron i is therefore
This quantity is obtained using a Monte Carlo integration as described
above. The Metropolis algorithm is used to sample the
probability distribution 
, where 
is the wavefunction
described in the previous section, and the estimator
is accumulated over the simulation to give the kinetic energy of electron i.
The calculation of 
is
actually performed in two parts due of the form of the wavefunction
being used. The trial wavefunction involves exponentials of the
functions u(r) and which make it convenient to deal with logarithms
of the wavefunction rather than differentiating the wavefunction
directly. Defining
and
then
If one considers the trial wavefunction in Eq.(
),
introduced in the previous section, then
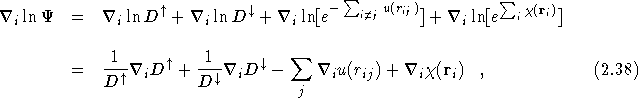
and
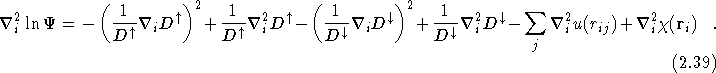
and 
are calculated from these equations at each step in
the random walk. The kinetic energy as given by Eq.(), is also
calculated at each step and averages of all three quantities are found
at the end of the simulation. The consistency of these three is
checked using Green's relation, which shows that
for all properly sampled wavefunctions. This consistency check is
extremely useful when debugging a QMC code. If either the first or
second derivative of the wavefunction has been calculated incorrectly,
this will immediately show up in this consistency check and it is
often clear which of the derivatives is being evaluated wrongly. The
variances of 
and 
are both much
greater[26, 23] than the variance of the kinetic energy as
given by Eq.(), therefore it is this quantity which is used to
estimate the kinetic energy in Monte Carlo calculations.
