The method we have used to sample points from the chosen probability
distribution, g(x), is the Metropolis algorithm[19]. In
this algorithm, a random walk is performed through the configuration
space of interest. The walk is designed so that the points on the
walk are distributed according to the required probability
distribution. At each point on the walk a random trial move from the
current position in configuration space is selected. This trial move
is then either accepted or rejected according to a simple
probabilistic rule. If the move is accepted then the ``walker'' moves
to the new position in configuration space; otherwise the ``walker''
remains where it is. (By a ``walker'' we mean a point in the
3N-dimensional configuration space of the problem.) Another trial
step is then chosen, either from the new accepted position or from the
old position if the first move was rejected, and the process is
repeated. In this way it should be possible for the ``walker'' to
explore the whole configuration space of the problem. The Metropolis
algorithm provides a prescription for choosing which moves in
configuration space to accept or reject. Suppose that the current
position on the random walk is 
, where defines the
positions of all the electrons in the system
and that the move, chosen randomly, would make the new position the
point 
. Each of these points has a number density associated
with it, 
and 
. The number density is simply
proportional to the probability distribution of that point in
configuration space. If the average over many steps of the random walk
follows the specified probability distribution then the walk is said
to have reached equilibrium. In this case, the average number
densities of points on the walk at and ,
and , should be constant. That means that
the probability of making a transition from to
has to be equal to the probability of making a transition in the
opposite direction, from to . The transition
probability of a trial move being made from to is
denoted by 
and the transition probability of a trial move being made
from to by 
. The trial moves are chosen from a fixed probability
distribution around the current position and since there is nothing
special about the points or ,
The probability of a trial move from to being
accepted is 
and the
probability of accepting the reverse move is 
. Total probabilities for moves
occurring in either direction are then
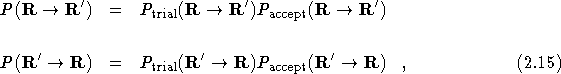
and the equilibrium condition implies that
In the Metropolis algorithm the probability of accepting the random
move, , is chosen to be
This satisfies the equilibrium conditions for the distribution. The
mechanism for accepting a move with probability
, within the QMC code, is to generate
a random number in the range [0,1]. If this random number
is less than then the move is
accepted. If this random number is greater than
then the move is rejected.
The above description was for a configuration space in which any one point could be reached from any other point in one move. If the configuration space is very large, then if small moves are made it is not possible to reach any other point in one move. As long as any one point can be reached from any other point the random walk is said to be ergodic and the Metropolis algorithm is still valid. A straightforward extension of the above argument can be made to justify the use of the Metropolis algorithm in this situation. To ensure that points are sampled correctly from the probability distribution, the random walk has to be allowed to proceed from some arbitrary initial starting point until the average over an ensemble of moves represents the distribution to be sampled. At this point equilibrium has been reached. It is only at this point that the importance sampling Monte Carlo calculation can be carried out. It should be noted that the Metropolis algorithm is just one of a large number of such algorithms, but we have not found any reason to choose a different algorithm.