In the flow chart of the VMC algorithm, (figure 
), it is
simply stated that the energy of the walker is accumulated after
moving each of the electrons. In fact we choose a slightly more
complicated formula for updating each of the quantities being
calculated[26]. After each proposed move, whether
it is rejected or not, each quantity <Q> is updated such that
where 
is any quantity of interest such as the kinetic energy,
potential energy or total energy associated with particle i, and p
is the probability of accepting the move from 
to
. It is possible simply to accumulate 
at
just the new points on the walk, but the combination in
Eq.(), of values at the old and new points allows
information about points which are rejected to be included and reduces
the contribution from ``unlikely'' moves which are accepted. By this
means, the variance of the expectation value of Q is reduced. It has
been shown in Ref.[26] that the accumulation of
gives a correct
sampling of the probability density, 
. This can be
demonstrated by considering each term, 
, and
, separately and calculating the probability
distribution which each term samples. By adding together these two
probability distributions, it is shown that the combination of the two
terms does indeed sample from the correct total probability
distribution.
is the energy of particle i when the configuration is
at 
The probability of being in configuration 
and evaluating the
energy of particle i, i.e. the probability of arriving at
configuration as a result of making a move of particle i
to 
, should obviously be 
if the sampling
is being done correctly.
At the old position of electron i, 
,
electron i can move anywhere within the range of the maximum step
size, i.e. within a volume V. The probability of
arriving at 
from 
is
. The probability of
evaluating 
after accepting a move
is therefore
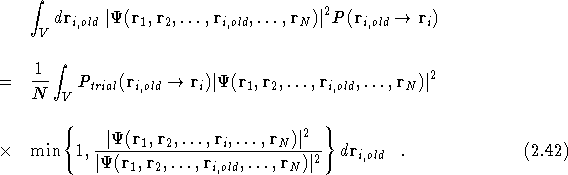
The probability of being at and rejecting any move
is
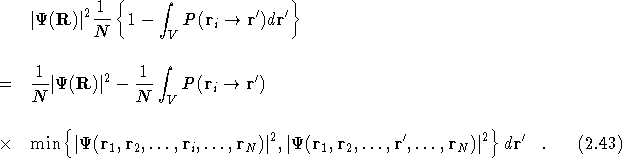
The sum of these two probabilities, i.e. accumulating 
as in
Eq.(), gives the probability density
, as required.
