Each time a single electron move is accepted, the value of the Slater
determinant changes. Recalculating the determinant after
each move is potentially an extremely costly procedure. Fortunately,
there is a method for updating the wavefunction[115, 26]
which is much less costly than recalculating the whole determinant
every time an electron is moved. The procedure is described here for
the specific case of moving a single electron, with spin 
,
from position 
to position 
. The
method is the same for all electrons and spins.
The quantity that is calculated is the ratio of the new and old determinants. From this ratios, the probability of acceptance of the move can be calculated. The cost of updating the quantities involved in the determinant, if the move is accepted, is greatly reduced by making use of this ratio.
The determinant 
only involves spin
electrons and therefore is not changed by the
move. 
is changed. The matrix
has elements
where 
are the set of N single-particle wavefunctions making
up the Slater determinant. When the electron is moved it is only the
i 
column of the matrix which changes.
One way of calculating the determinant of any matrix, 
, is to use the
relation
where 
is the unit matrix, 
is the transpose of matrix
and 
is the matrix of cofactors of matrix . The
determinant can be calculated by choosing any column, i, of the matrix
and summing
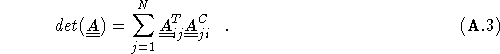
For the particular case of moving electron i, it is only the
column of which is altered and this does
not change any elements of the column of the matrix
. The determinant after the move has been made,
, can be written as
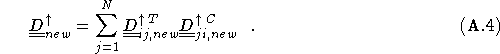
If the transpose of the inverse matrix is denoted by
then, from the definition of the inverse
of a matrix,
so
The new determinant, 
, is written as
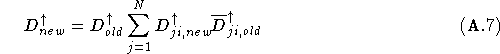
and the calculation of the ratio 
is simply
This ratio, 
, is the quantity which is required when calculating the
probability of the move being accepted.
If the move of electron i, with spin s, is accepted then the
matrix 
is updated in the following manner
The case where k = i comes simply from the definition of
in Eq.(
). Finding the updated
matrix elements when 
is more
complicated.
The new determinant matrix, 
, is written
as the old determinant matrix, 
, plus a perturbation matrix,
. Therefore
where
The following matrix identity is used to find the inverse of a sum of two matrices,
[This identity can be proved by multiplying on the left by (A +B).] Hence,
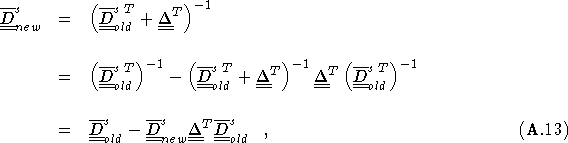
which can be written in terms of matrix elements as
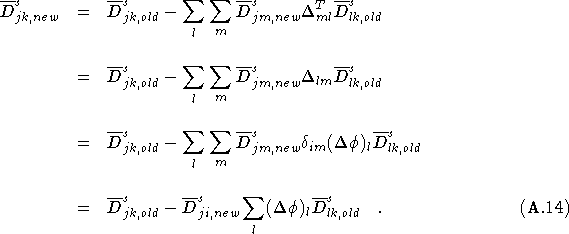
Using the definition of the matrix elements of 
for the case of k = i, as defined in Eq.() and
expanding out 
, the equation
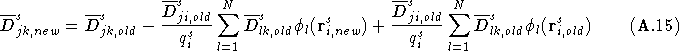
is obtained. The last term in the above equation
is
simply the matrix multiplication 
which gives
. However in this case so the last term is
zero. The update equation reduces to
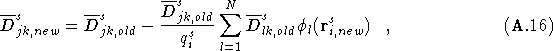
as required.
