Monte Carlo methods are a way of using random numbers to perform numerical integrations. By way of example consider the integral
There are many quadrature methods, with varying degrees of accuracy,
which can be used to evaluate this integral. The trapezium rule and
Simpson's method (see ``Numerical Recipes'', [18])
are both quadrature methods which involve evaluating f(x) at evenly
spaced points, 
, on a grid. A weighted average of these values
gives an estimate of the integral
where the 
are the weights. The weights and the sampling points
are different for different methods of quadrature but all the methods
sample the function f(x) using pre-determined weights and sampling
points.
Monte Carlo methods do not use specific sampling points but instead we choose points at random. The Monte Carlo estimate of the integral is then,
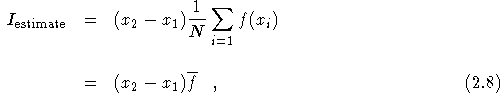
where the are randomly sampled points and 
is the
arithmetic mean of the values of the function f(x) at the sampling
points. The standard deviation of the mean is given by
where
gives an estimate of the statistical error in the Monte Carlo estimate
of the integral. Note that the error goes as 
,
independent of the dimensionality of the integral.
