John Biggins

Dr John Biggins
University Lecturer
Fellow of Corpus Christi College
Visitor
Office: 505 Mott Bld
Phone: +44(0)1223 3 37380
Email: jsb56 @ cam.ac.uk
Personal web site
TCM Group, Cavendish Laboratory
19 JJ Thomson Avenue,
Cambridge, CB3 0HE UK.
Research
Soft Mechanics
I am an Associate Professor in Cambridge University's Engineering Department, where I hold a UKRI Future Leaders Fellowship, and run the Soft Mechanics research group. I am currently a visitor in TCM, having previously worked here as an early career lecturer, research fellow and PhD student.
I am recruiting PhD students - if you are interested, send me an email.
Soft solids are found throughout biology and engineering - we eat them, sleep on them and are made out of them. Familiar examples include rubber, jelly, sponge, muscle and skin. I lead the soft mechanics group, which is focused on the mechanics of these materials: how do they deform, contort and fail? The hallmark of such soft solids is that they can deform substantially, and in response to slight and diverse stimuli. Their solid mechanics is correspondingly rich and dramatic, with many examples of spectacular shape changing phenomena for us to understand, and ultimately use in shape-shifting devices.
My group is particularly interested in liquid crystal elastomers, a remarkable new phase of matter that combines the mobile orientational order of liquid crystals with the extreme stretchiness of rubber. These materials can actively contract by a large factor on stimulation by heat or light, making them attractive artificial muscles.
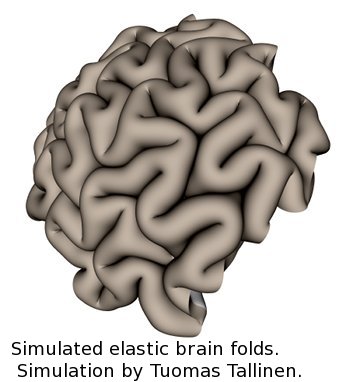
Even simple soft solids, such as conventional rubber, can deform in dramatic and unexpected ways. For example, if you if you start to blow up a cylindrical party balloon you will see a propagating bulge, and if you squeeze the skin on your arm you will see the formation of wrinkles. These phenomena are examples of elastic instabilities, and are similar in spirit to the classic Euler buckling instability in columns under compression. However, such instabilities are much more interesting in highly deformable soft solids, both because there are many more examples, and because soft solids can survive such instabilities, allowing them to be functional rather than simply failure modes. For example, evolution has harnessed a compressive wrinkle-like instability to sculpt the gyri and sulci of the human brain during development!
Finally, I also explained the chain fountain.

In Plain English
When an elastic structure is pushed or pulled it responds by changing shape. For example, if you pull on the two ends of an elastic band it gets longer. For small forces the shape changes are typically simple and small, but if you apply enough force the structure sometimes responds by changing shape in dramatic and unexpected ways, forming complicated shapes from simple ones. I discover and describe these shape dramatic changes.
During biological development a basically spherical egg turns into a complex assemblage of complicated shapes known as an organism. I also investigate whether these complicated shapes form via such elasticity. For example, one small part of development is the formation of iconic the folded surface of the brain. I am investigating whether this is simply because the outside of the brain grows faster than the inside, and consequently crumples up.
I also explained the chain fountain.
Featured Publications
-
Metric mechanics with non-trivial topology: actuating irises, cylinders
and evertors
Phys. Rev. E
104
065004
(2021)
- Magnesium Nanoparticle Plasmonics. Nano Lett. 18 3752 - 3758 (2018)
- The Plateau-Rayleigh instability in solids is a simple phase separation Phys. Rev. E 95 053106 (2017)
- Pattern selection when a layer buckles on a soft substrate. Soft Matter 15 3751 - 3770 (2019)
- Localized soft elasticity in liquid crystal elastomers. Nat Commun 7 10781 (2016)
- Peristaltic elastic instability in an inflated cylindrical channel Phys. Rev. Lett. 122 068003 (2019)
- Mechanics of invagination and folding: Hybridized instabilities when one soft tissue grows on another Phys. Rev. E 92 (2015)
- Mechanics of mouse blastocyst hatching revealed by a hydrogel-based microdeformation assay P. Natl Acad. Sci. USA 115 10375 - 10380 (2018)
- Gyrification from constrained cortical expansion. P. Natl. Acad. Sci. USA 111 12667 - 12672 (2014)
- Exactly isochoric deformations of soft solids Europhys. Lett. 108 64001 (2014)
- Understanding the chain fountain Proc. Royal Soc. A - Math. Phy. 470 20130689 (2014)
- Digital instability of a confined elastic meniscus P. Natl. Acad. Sci. USA 110 12545 - 12548 (2013)
- Surface sulci in squeezed soft solids. Phys. Rev. Lett. 110 024302 (2013)
- Supersoft Elasticity in Polydomain Nematic Elastomers (vol 103, 037802, 2009) Phys. Rev. Lett. 104 089901 (2010)