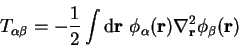Total energy and Hamiltonian

A quantity which is frequently required is the overlap matrix 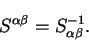$S_{\alpha \beta}$ defined by

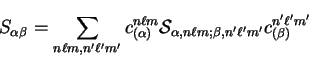$$S_{\alpha \beta} = \int {\mathrm d}{\bf r}~ \phi_{\beta}({\bf r}) \phi_{\alpha}({\bf r}) .$$ (7.3)

The overlap matrix elements between the spherical-wave basis functions can be calculated analytically (section 5.4), and are denoted 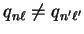${\cal S}_{\alpha, n \ell m ; \beta, n' \ell' m'}$ where

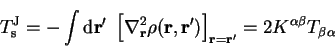$${\cal S}_{\alpha , n \ell m ;\beta , n' \ell' m'} = \langle ... ..._{\alpha , n \ell m} \vert \chi_{\beta , n' \ell' m'} \rangle$$ (7.4)

so that the overlap matrix elements are given by

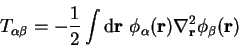$$S_{\alpha \beta} = \sum_{n \ell m, n' \ell' m'} c^{n \ell m}... ...pha , n \ell m ;\beta , n' \ell' m'} c^{n' \ell' m'}_{(\beta)}$$ (7.5)

recalling that the support functions may be assumed real in the case of 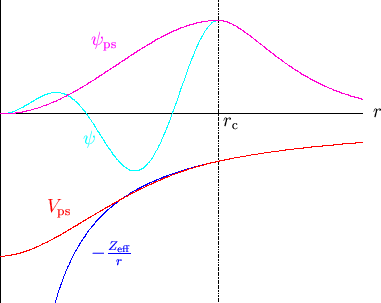$\Gamma$-point Brillouin zone sampling.