



Next: Local pseudopotential
Up: Total energy and Hamiltonian
Previous: Hartree energy and potential
Contents
Having calculated the electron density on the grid points, the exchange-correlation energy is obtained by summing over those grid points
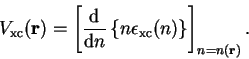 |
(7.12) |
in the local density approximation. 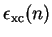 is the volume of the supercell divided by the number of grid points. The exchange-correlation potential is
similarly calculated at each grid point as
is the volume of the supercell divided by the number of grid points. The exchange-correlation potential is
similarly calculated at each grid point as
![\begin{displaymath}
V_{\mathrm {xc}}({\bf r}) = \left[ \frac{\mathrm d}{{\mathrm...
...\epsilon_{\mathrm {xc}}(n) \right\} \right]_{n = n({\bf r})} .
\end{displaymath}](img944.gif) |
(7.13) |
In practice, the values of
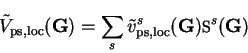 and
and
![$\frac{\mathrm d}{{\mathrm d}n} \left[
n \epsilon_{\mathrm {xc}}(n) \right]$](img946.gif) are tabulated for various values of
the electronic density
are tabulated for various values of
the electronic density  and then interpolated during the calculation.
and then interpolated during the calculation.
Peter D. Haynes
1999-09-21
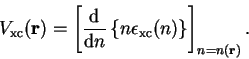
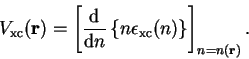
![\begin{displaymath}
V_{\mathrm {xc}}({\bf r}) = \left[ \frac{\mathrm d}{{\mathrm...
...\epsilon_{\mathrm {xc}}(n) \right\} \right]_{n = n({\bf r})} .
\end{displaymath}](img944.gif)