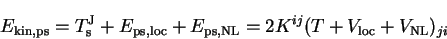Next: Energy gradients
Up: Total energy and Hamiltonian
Previous: Local pseudopotential
Contents
The non-local pseudopotential energy is given by
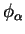 |
(7.18) |
The matrix elements of the non-local pseudopotential in the representation of
the support functions
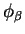 are calculated by
summing over all ions whose cores overlap the support regions of
are calculated by
summing over all ions whose cores overlap the support regions of
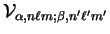 and
and 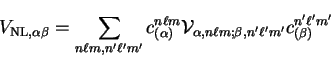 , and using the method described in
section 5.6.2 to calculate the spherical-wave basis function
matrix elements
, and using the method described in
section 5.6.2 to calculate the spherical-wave basis function
matrix elements
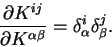 analytically. The result is therefore
analytically. The result is therefore
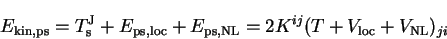 |
(7.19) |
which is of exactly the same form as the kinetic energy, so that in practice
the basis function matrix elements for the kinetic energy and non-local
pseudopotential are summed and the two contributions to the energy combined.
Peter D. Haynes
1999-09-21