Next: Hartree energy and potential
Up: Total energy and Hamiltonian
Previous: Total energy and Hamiltonian
Contents
The kinetic energy of the non-interacting Kohn-Sham system is given by
![\begin{displaymath}
T_{\mathrm s}^{\mathrm J} = - \int {\mathrm d}{\bf r'}~
\lef...
...ight]_{{\bf r}={\bf r'}}
= 2 K^{\alpha \beta} T_{\beta \alpha}
\end{displaymath}](img932.gif) |
(7.6) |
in which
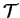 |
(7.7) |
are the matrix elements of the kinetic energy operator in the representation
of the support functions. Since all of the matrix elements between the
spherical-wave basis functions can be calculated analytically,
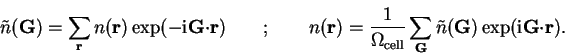 |
(7.8) |
where 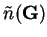 denotes matrix elements of the kinetic energy
operator between spherical-wave basis functions.
denotes matrix elements of the kinetic energy
operator between spherical-wave basis functions.
Peter D. Haynes
1999-09-21