



Next: Non-local pseudopotential
Up: Total energy and Hamiltonian
Previous: Exchange-correlation energy and potential
Contents
Like the Hartree potential, the local pseudopotential is also calculated in
reciprocal-space as
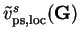 |
(7.14) |
where the summation is over ionic species 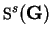 ,
,
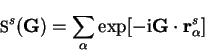 is the local pseudopotential for an isolated ion of species
is the local pseudopotential for an isolated ion of species 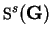 in
reciprocal-space and
in
reciprocal-space and
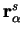 is the structure factor for
species
is the structure factor for
species 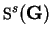 defined by
defined by
![\begin{displaymath}
{\mbox{\Bbb S}}^s({\bf G}) = \sum_{\alpha} \exp[-{\mathrm i}{\bf G} \cdot {\bf r}_{\alpha}^s]
\end{displaymath}](img951.gif) |
(7.15) |
where the sum is over all ions  of species
of species 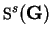 with positions
with positions
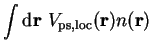 .
We note that in general the calculation of the structure factor is
an
.
We note that in general the calculation of the structure factor is
an 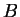 operation, but since it only has to be calculated once
for each atomic configuration, it is not a limiting factor of the overall
calculation at this stage. Within the quantum chemistry community,
work on generalised multipole expansions and new algorithms
[156,157,158,159,160,161,162]
has led to the development of methods to calculate Coulomb
interaction matrix elements which scale linearly with system-size.
The local pseudopotential energy can be calculated in reciprocal-space as
operation, but since it only has to be calculated once
for each atomic configuration, it is not a limiting factor of the overall
calculation at this stage. Within the quantum chemistry community,
work on generalised multipole expansions and new algorithms
[156,157,158,159,160,161,162]
has led to the development of methods to calculate Coulomb
interaction matrix elements which scale linearly with system-size.
The local pseudopotential energy can be calculated in reciprocal-space as
where
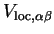 is the pseudopotential core energy, and
is the pseudopotential core energy, and
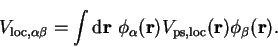 the number of ions of species
the number of ions of species 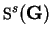 . The matrix elements
. The matrix elements
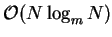 are defined by
are defined by
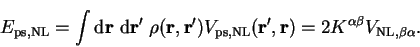 |
(7.17) |
The Hartree potential and local pseudopotential can be summed and then
transformed back
together into real-space and added to the exchange-correlation potential to
obtain the local part of the Kohn-Sham potential in real-space.
We note that the FFT is not strictly an 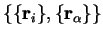 operation but an
operation but an
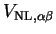 operation
(where
operation
(where 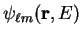 is some small number which depends upon the prime factors of the
number of grid points), but in practice (section 9.2)
this scaling is not observed.
is some small number which depends upon the prime factors of the
number of grid points), but in practice (section 9.2)
this scaling is not observed.




Next: Non-local pseudopotential
Up: Total energy and Hamiltonian
Previous: Exchange-correlation energy and potential
Contents
Peter D. Haynes
1999-09-21
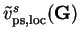
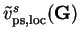
![\begin{displaymath}
{\mbox{\Bbb S}}^s({\bf G}) = \sum_{\alpha} \exp[-{\mathrm i}{\bf G} \cdot {\bf r}_{\alpha}^s]
\end{displaymath}](img951.gif)
![]() operation but an
operation but an
![]() operation
(where
operation
(where ![]() is some small number which depends upon the prime factors of the
number of grid points), but in practice (section 9.2)
this scaling is not observed.
is some small number which depends upon the prime factors of the
number of grid points), but in practice (section 9.2)
this scaling is not observed.