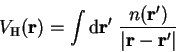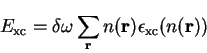Next: Exchange-correlation energy and potential
Up: Total energy and Hamiltonian
Previous: Kinetic energy
Contents
The Hartree and exchange-correlation terms are calculated by
determining the electronic density on a real-space
grid  , and Fast Fourier Transforms (FFTs) are used to transform between
real- and reciprocal-space7.1to obtain
, and Fast Fourier Transforms (FFTs) are used to transform between
real- and reciprocal-space7.1to obtain
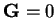 . The Hartree energy is then given by
. The Hartree energy is then given by
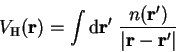 |
(7.9) |
where
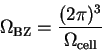 is the volume of the supercell and the
(infinite)
is the volume of the supercell and the
(infinite) 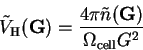 term is omitted because the system is charge neutral
overall. This term is therefore cancelled by similar terms in the ion-ion
and electron-ion interaction energies. The Hartree potential in real-space is
given by
term is omitted because the system is charge neutral
overall. This term is therefore cancelled by similar terms in the ion-ion
and electron-ion interaction energies. The Hartree potential in real-space is
given by
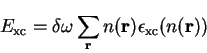 |
(7.10) |
but is calculated in reciprocal-space as
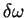 |
(7.11) |
and then transformed back into real-space by a FFT.
Peter D. Haynes
1999-09-21
![]() , and Fast Fourier Transforms (FFTs) are used to transform between
real- and reciprocal-space7.1to obtain
, and Fast Fourier Transforms (FFTs) are used to transform between
real- and reciprocal-space7.1to obtain
![]() . The Hartree energy is then given by
. The Hartree energy is then given by