The Trial Wavefunction

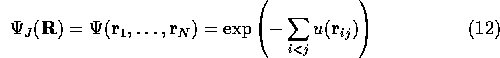
The u(r) function is chosen to minimise the energy of the state by increasing the probability of He atoms being separated by a distance where their interaction energy is a minimum. The kinetic energy is increased due to confinement but the total energy is still reduced.

The work presented in this report is exclusively concerned with fermion problems where the many-body wavefunction is an anti-symmetric function of the positions of the particles. The simplest anti-symmetric function one can choose is the Slater determinant known as the Hartree-Fock approximation. This function incorporates the exchange interaction between electrons but takes no account of the correlation between them, i.e. for electrons of opposite spin there is no repulsion term in the Slater determinant. Therefore, a Jastrow function is again included in the wavefunction to introduce the effects of correlation between electrons. The Jastrow function takes the same form as in () where u(r) is written as

The variational parameters A and F in Eqn.() are chosen to satisfy the cusp condition [2]. This specifies that

The trial wavefunction can therefore be written as

The Slater determinant D has been written as the product of two individual Slater determinants , one for spin up electrons and one for spin down electrons given by

where are the set of N single-particle wavefunctions obtained from the corresponding LDA calculation.

It has been found that the introduction of the two-body Jastrow function into the fermionic wavefunction has two main effects:-

• It decreases the interaction energy due to the introduction of correlation and increases the kinetic energy due to confinement. The overall effect is to lower the total energy of the system as was the case for bosonic systems.
• It tends to make the charge density more uniform than that obtained from the Slater determinant alone, reducing the charge density in higher density regions and increasing it in lower density regions.

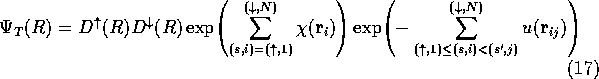
The one-body term, çould formally be incorporated into the Slater determinant by multiplying each single-particle wavefunction by 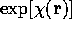, but it is left as a separate function so that it can be individually optimised. The form of and possible schemes for optimising it are discussed at length in section .