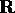sampled from 
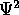first start with a
randomly distributed set of
positions 
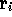. Then move each particle by a vector 
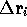chosen from a Gaussian distribution centred on a sphere of radius 'step size',
to a new trial position,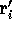 
.
This new trial position is then accepted with probability P,
where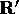 
is a configuration with the 
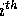particle at 
.
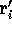If a move is rejected then the old configuration R
becomes the new
configuration R
', otherwise R
' becomes the new configuration.
After a large enough number of moves the positions of the particles
within configuration R
will become asymptotically distributed
according to 
.
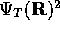The proof of the Metropolis algorithm can be summarised as follows.
Consider a whole set of configurations evolving according to the
Metropolis algorithm. When they have reached equilibrium the number of
configurations moving from R
to R
' is equal to the number walking
from R
' to R
and therefore
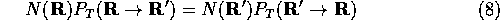
Now at equilibrium
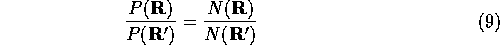
Therefore the rule for accepting a move is
One, of many, ways of satisfying this relationship is to allow the probability of moves according to
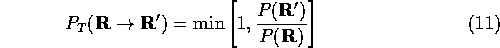
The most important advantage of using the Metropolis algorithm in QMC
calculations is the fact that the condition for accepting or rejecting a
move of an electron depends on the ratio of the value of the
wavefunction at two points in space, not the absolute values at those points.
Calculating this ratio can be shown [9] to take only order N arithmetic
operations, where N is the number of electrons in the system. This is
