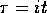 .
.



The idea behind the scheme is to write the Schrödinger equation in
imaginary time, 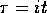 .
.
Now 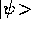 can be expanded in terms of the the eigenstates
of the time-independent Schrödinger equation,
can be expanded in terms of the the eigenstates
of the time-independent Schrödinger equation, 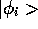 .
.
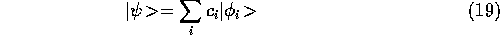
The formal solution to ( ) can then be written as.
) can then be written as.
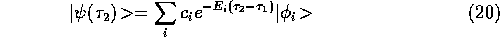
where 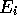 are the eigenvalues corresponding to
are the eigenvalues corresponding to 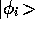 .
Now let
.
Now let 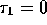 and hence
and hence 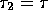 . The
evolution through time implies that as long as
. The
evolution through time implies that as long as 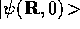 is not
orthogonal to
is not
orthogonal to 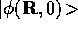 then
then
where 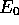 is the ground state energy of the system. All the other
eigenstates of the system will decay faster than the ground state due
to their higher energies.
is the ground state energy of the system. All the other
eigenstates of the system will decay faster than the ground state due
to their higher energies.
If an energy shift is introduced into the imaginary time Schrödinger
equation ( ) so that
) so that
and the energy shift 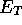 is adjusted to be the ground state energy
is adjusted to be the ground state energy
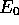 then using (
then using ( ) it can be seen that the
asymptotic solution to (
) it can be seen that the
asymptotic solution to ( ) is a steady state solution that is
the exact ground state of the system.
) is a steady state solution that is
the exact ground state of the system.
Eqn.( ) can be solved for the ground state using a
simulation based on a combination of diffusion and branching processes
where
) can be solved for the ground state using a
simulation based on a combination of diffusion and branching processes
where 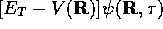 is the rate term describing the
branching process. This describes how the number of diffusers increases
or decreases in proportion to the density of existing diffusers.
is the rate term describing the
branching process. This describes how the number of diffusers increases
or decreases in proportion to the density of existing diffusers.
In practice, solving ( ) in this way is very inefficient because
the branching rate which is proportional to V( R
) can diverge to
) in this way is very inefficient because
the branching rate which is proportional to V( R
) can diverge to
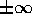 , leading to large fluctuations in the number of diffusers.
Therefore, importance sampling is introduced in the form of a new
distribution
, leading to large fluctuations in the number of diffusers.
Therefore, importance sampling is introduced in the form of a new
distribution 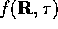 using a guiding function,
using a guiding function, 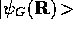
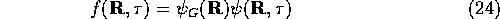
The imaginary time Schrödinger equation ( ) now becomes
) now becomes
Where 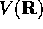 is a drift velocity,
is a drift velocity, 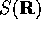 is the new branching term
equal to the excess local energy,
is the new branching term
equal to the excess local energy, 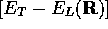 , and
, and 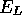 is the
local energy of the guiding
function,
is the
local energy of the guiding
function, 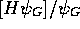 . If the guiding wavefunction,
. If the guiding wavefunction, 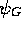 is
chosen so that
is
chosen so that 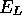 is as uniform as possible everywhere then the
branching process is considerably reduced thereby improving the
efficiency of the calculation. Possible methods of reducing the
variance of
is as uniform as possible everywhere then the
branching process is considerably reduced thereby improving the
efficiency of the calculation. Possible methods of reducing the
variance of 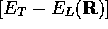 are discussed at length in section
are discussed at length in section
 .
.
The scheme for solving ( ) is given in detail in Ceperly's
paper [3], so only an outline will be given here as it
is not directly relevant to the work in this report.
) is given in detail in Ceperly's
paper [3], so only an outline will be given here as it
is not directly relevant to the work in this report.
Eq. ( ) can be written in integral form
) can be written in integral form
In general 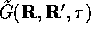 is not known, but reliable
approximations can be derived for small values of
is not known, but reliable
approximations can be derived for small values of  .
In a DMC calculation, instead of solving (
.
In a DMC calculation, instead of solving ( ) directly, one
proceeds step-by-step in time, repeatedly applying
Eqn.(
) directly, one
proceeds step-by-step in time, repeatedly applying
Eqn.( ) for small values of
) for small values of  .
.
The three terms on the left of ( ) describe
diffusion, drift and growth,decay. An approximate Greens function can
therefore be formed, with an error of
) describe
diffusion, drift and growth,decay. An approximate Greens function can
therefore be formed, with an error of 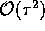 for small
for small
 , by the product of the Green's functions for diffusion, drift and
growth,decay.
, by the product of the Green's functions for diffusion, drift and
growth,decay.
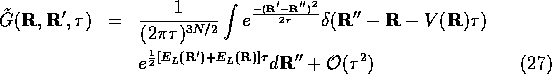
The remaining problem to be solved is that of determining a suitable
guiding wavefunction, 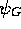 . This determines the positions of
the nodes of the final wavefunction
as
. This determines the positions of
the nodes of the final wavefunction
as 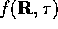 approaches
approaches 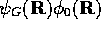 at long times.
The ground state energy
at long times.
The ground state energy 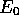 obtained by the DMC calculation will only be
the exact groundstate energy of the system if the nodes of
obtained by the DMC calculation will only be
the exact groundstate energy of the system if the nodes of 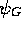 agree exactly with the nodes of the true ground state wavefunction.
In practice, this fixed node approximation often introduces the most
significant error into DMC calculations, although the statistical error
is also large.
agree exactly with the nodes of the true ground state wavefunction.
In practice, this fixed node approximation often introduces the most
significant error into DMC calculations, although the statistical error
is also large.


