Research Highlights
Non-Hermitian topology corresponds to directional amplification
The authors show that non-trivial values of a topological invariant, a winding number defined on the spectrum of the non-Hermitian dynamic matrix, correspond to directional amplification in driven-dissipative cavity arrays.
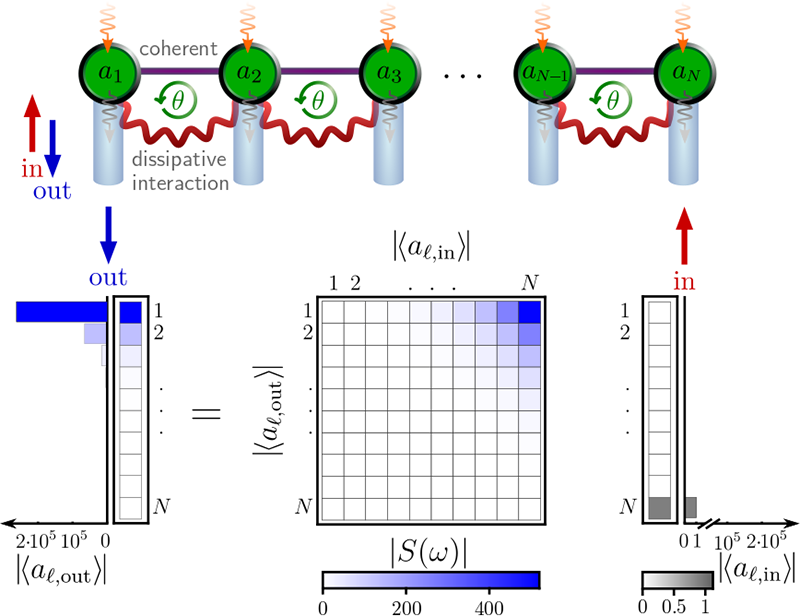
Chain of driven-dissipative cavities, whose nearest neighbours are coupled both coherently and dissipatively, directionally amplifies a coherent signal if the winding number associated with the spectrum of the system's dynamic matrix is non-trivial. This is then quantified by the highly asymmetric scattering matrix with large gain.
Directional amplification is a key resource for information processing applications. It allows to amplify weak signals while protecting the fragile signal source, e.g. superconducting qubits, against noise in the reverse direction. In their article, the authors uncover a one-to-one correspondence between non-trivial values of a winding number defined on the non-Hermitian dynamic matrix and directional amplification in driven-dissipative cavity arrays. They derive an analytic expression for the scattering matrix proving that the end-to-end gain in non-trivial regimes grows exponentially with the system size whereas the reverse gain is exponentially attenuated. Their analysis serves as a general recipe for designing novel multimode amplifiers on the basis of several experimental platforms, such as superconducting circuits, optomechanical systems, and topolectric circuits, and as such is of high experimental relevance.
Topological framework for directional amplification in driven-dissipative cavity arrays CC Wanjura, M Brunelli & A Nunnenkamp, Nat Commun 11, 3149 (2020).