Figure 1. Schematic representation of the supercell calculation of a small molecule adsorption on a surface
This section provides information specific to the implementation of DFT in the CASTEP program. A general overview of DFT is provided elsewhere. The general overview provides information on the concepts of charge density, DFT functionals, the SCF procedure, and band structures, which are applicable to any computational implementation of DFT. The application of dispersion corrections to DFT is also described.
In contrast, this section provides background information on aspects of DFT that are specific to CASTEP.
The CASTEP program provides a robust and efficient implementation of DFT which is based on the following concepts:
Some of these topics are expanded on in this section. More detailed information can be found in the links listed at the end of this topic.
CASTEP is based on a supercell method, wherein all studies must be performed on a periodic system, even when the periodicity is superficial. Thus, for example, a crystal surface must be represented by a finite-length slab (Figure 1). Similarly, to study molecules it is necessary to assume that they are in a box and treat them as periodic systems. There is no limitation on the shape of the supercell.
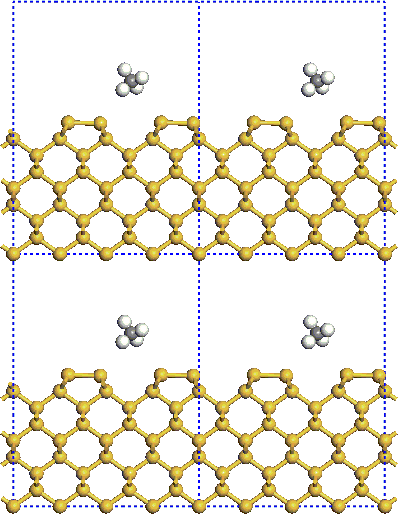
Figure 1. Schematic representation of the supercell calculation of a small molecule adsorption on a surface
The main advantage of imposing periodic boundary conditions relates to Bloch's theorem, which states that in a periodic system each electronic wavefunction can be written as a product of a cell-periodic part and a wavelike part (Payne et al. 1992):
Eq. CASTEP 1
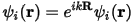
The cell periodic part, ψ, can then be expanded using a basis set consisting of a discrete set of plane waves whose wave vectors are reciprocal lattice vectors of the crystal:
Eq. CASTEP 2
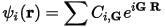
Therefore, each electronic function can be written as a sum of plane waves, exp[i(k+G)•R]. Advantages and technical details of the plane wave basis set are described in a separate section.
Among the major gains is the simplified form of the Kohn-Sham equations:
Eq. CASTEP 3
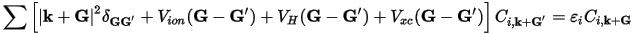
In this form, the kinetic energy is diagonal, and the various potentials (electron-ion, Hartree, exchange-correlation) are described in terms of their Fourier transforms.
Another advantage of the plane wave basis set is the ease of calculating derivatives of the total energy with respect to atomic displacements (that is, stresses and forces are computationally cheap in this approach), so that efficient geometry optimization and molecular dynamics schemes can be implemented. It is also straightforward to study and improve convergence of plane-wave basis set calculations, as there is a systematic way of adding more basis functions.
However, there is an additional cost to using the supercell approach for systems that lack periodicity in three dimensions inherently (isolated molecules, defects in solids, surfaces, and so on). In a study of a single defect, for example, the properties of an infinite array of defects (Figure 2) would always be calculated. Therefore, it is essential to introduce enough separation between artificial images of such nonperiodic objects to ensure that there is no appreciable interaction between them. The situation is similar for surface calculations that are carried out in a slab geometry. The vacuum layer should be sufficiently thick to eliminate artificial interactions between the slabs.
Figure 2. Schematic representation of the supercell calculation of a substitutional impurity in a bulk
One of the major computational steps in CASTEP is the calculation of the product of the Hamiltonian with a wavefunction, Hψ. It has been shown above that the kinetic energy operator of the Hamiltonian has a diagonal representation in reciprocal space. The same is true of the Hartree operator and of the local pseudopotential operator. Exchange-correlation potential, on the other hand, has a diagonal representation in real space. This means that there is a need for an efficient way of transforming various entities (wavefunctions, potentials, search directions) from real to reciprocal space and back. FFT provide this, so that the gain due to the evaluating various parts of the Hamiltonian in their "natural" representations is not offset by the cost of the transformation.
CASTEP implements a number of exchange-correlation functionals: local (LDA), gradient-corrected (GGA), and fully nonlocal (based on the exact and screened exchange formalism).
The exchange-correlation energy is given by Eq. DFT 7. There is only one local functional provided in CASTEP, the Perdew and Zunger (1981) parameterization of the numerical results of Ceperley and Alder (1980), CA-PZ.
This particular prescription for the local representation of the exchange-correlation potential is considered to be one of the most accurate descriptions available (Srivastava and Weaire, 1987).
The so-called nonlocal or gradient-corrected functionals depend on dρ/dr as well as on ρ. This provides a considerable increase in the accuracy of predicted energies and structures, but with an additional cost. The nonlocal functionals available in CASTEP include:
| Name | Description | Reference |
|---|---|---|
| PW91 | Perdew-Wang generalized-gradient approximation, PW91 | Perdew and Wang |
| PBE | Perdew-Burke-Ernzerhof functional, PBE | Perdew et al. |
| RPBE | Revised Perdew-Burke-Ernzerhof functional, RPBE | Hammer et al. |
| WC | More accurate GGA functional, based on a diffuse radial cutoff for the exchange hole in real space and the analytical gradient expansion of the exchange energy for small gradients | Wu and Cohen |
| PBEsol | A version of the PBE functional that improves equilibrium properties of densely packed solids and their surfaces | Perdew et al. |
| BLYP | Becke exchange, Lee-Yang-Parr correlation | Becke; Lee, Yang, Parr |
The PBE functional has been designed to give essentially the same results as the PW91 functional but it is more robust in systems with rapidly varying electron density. The RPBE functional has been designed specifically to improve the DFT description of the adsorption energies of molecules on metallic surfaces (for a detailed comparison of these three functionals when applied to surface science problems see Marlo and Milman, 2000). One of the latest developments, PBEsol functional, is explicitly designed to improve the first-principles gradient expansion for exchange over a wide range of density gradients, and hence to improve the description of equilibrium properties of densely packed solids and their surfaces.
All gradient-corrected functionals in CASTEP are implemented according to the method described by White and Bird (1994). The application of gradient-corrected exchange-correlation functionals in total-energy calculations using a plane-wave basis set is less straightforward than in localized basis set approaches (used in other programs such as DMol3). The usual form of the exchange-correlation potential includes gradients whose calculation requires the use of a high-quality representation of the density which is computationally expensive in both memory and time. These problems are overcome by defining an exchange-correlation potential for the discrete set of grid points consistent with the discretized form of the exchange-correlation energy that is used in plane-wave total-energy calculations. This potential is calculated exactly on the minimum fast Fourier transform grid and gives improved convergence and stability as well as computational efficiency.
In addition to the generalized gradient (GGA) functionals, which depend on the local density and its gradient, CASTEP can handle functionals that depend on the kinetic energy density. The current supported functional is RSCAN (Bartók and Yates, 2019), which is an improved regularized version of the SCAN ("Strongly Constrained and Appropriately Normed") functional developed by Sun et al., 2016. Meta-GGA functionals are considered to be more accurate than pure GGA, and the cost of such calculations is significantly lower than for nonlocal functionals.
The SCAN functional satisfies all known constraints that a semi-local functional can satisfy, and the remaining free parameters are fitted to reproduce exact or accurate reference values, or norms, of exchange and correlation energies.
The RSCAN modification eliminates the unphysical divergence of the exchange-correlation potential, which occurs in some free atoms, and fixes the feature of the switching function in SCAN, which introduces rapidly oscillating regions in the exchange-correlation potential. These improvements are necessary to make the SCAN functional usable in the context of robust pseudopotential generation. CASTEP's implementation has shown that RSCAN is transferable and accurate for a broad range of solid state and molecular systems.
Currently, there are limitations on the use of meta-GGA in CASTEP. The meta-GGA functional is not compatible with DFT-D corrections, spin-orbit coupling, J-coupling , linear-response phonons, or polarizability calculations. The formalism cannot be used with mixture atoms. Only on the fly generated pseudopotentials can be used.
Kohn-Sham schemes based on LDA and GGA functionals have a common feature: they underestimate the band gap substantially. This does not affect the accuracy of the description of the total energy and related properties of crystals and molecules (equilibrium structure, vibrational spectra, elastic constants, and so on). However, an accurate description of the details of the electronic structure is often required to understand the properties of semiconductors and insulators. Then a DFT error of up to 50% in the calculated band gap energy becomes unacceptable.
It is possible to correct for the DFT band gap error by introducing an empirical scissors correction, which is effectively a rigid shift of the conduction band with respect to the valence band. This approach produces satisfactory results for such properties as optical spectra, provided the experimental band gap is accurate. The scissors operator scheme is very difficult to use in predictive studies and in the context of band gap engineering, when there is little or no experimental information about the electronic structure. In addition, the scissors operator approach does not help when an improvement in the description of the electronic structure of metallic systems is required.
There are a wide variety of techniques designed to deal with the band-gap problem in DFT. Most of them are exceedingly complex and time consuming. One of the most practical solutions is the so-called screened exchange, or sX-LDA scheme, developed in the context of the generalized Kohn-Sham procedure (Seidl et al., 1996). Generalized Kohn-Sham schemes allow one to split the exchange contribution to the total energy into a screened, nonlocal and a local density component.
The following generalized Kohn-Sham schemes are implemented in CASTEP:
The sX-LDA or HSE06 scheme is recommended for band gap calculations.
The implementation of screened exchange in CASTEP follows closely the recipe suggested by Seidl et al. (1996). The Thomas-Fermi screening function is used (the case of zero screening length, kTF, corresponds to the exact exchange formalism).
CASTEP provides a number of schemes for evaluating the screening length. The most straightforward to use is average density. This is a reasonable approach for bulk solids, but not for systems with large amounts of vacuum in the cell, for example molecules, surfaces, porous materials, and so on.
Alternatively, you can use the kTF value associated with the self-weighted average density of the system. The self-weighted average is given by the integral of the density squared divided by the integral of the density. This removes the problems connected with large regions of vacuum. Otherwise, you can evaluate the self-weighted average of the screened exchange energy density.
Nonlocal functionals have certain limitations compared with LDA and GGA functionals. For example, there is no known analytical expression for the stress tensor components in the exact exchange formalism. Thus, none of the fully nonlocal potentials can be used to optimize the unit cell of a crystal or to perform NPT/NPH dynamics (only sX-LDA, HSE03, or HSE06 functionals support stress calculations). It is also possible that the optical properties calculated using these functionals may be inaccurate. This problem is related to the introduction of a fully nonlocal component of the Hamiltonian. The addition of a nonlocal potential breaks the usual expressions for transforming the optical matrix element from the position operator to the momentum operator, because the commutator with the Hamiltonian becomes exceedingly complex (Asahi et al., 1999). However, even with the significant computational overhead of the screened exchange formalism, it provides a state of the art scheme for predictive studies of electronic and optical properties of crystals.
Nonlocal functionals are currently implemented only for norm-conserving potentials, not for ultrasoft ones.
There is an important difference between standard DFT calculations with local exchange-correlation potentials and the nonlocal exchange case. The potential used in the latter scenario depends on the SCF k-points, while in the former case, the potential depends only on electron density. This difference can make all properties calculations a lot more expensive in terms of memory usage and CPU time, so it is advisable to limit the number of SCF k-points that you use in such situations. This is particularly relevant for small unit cells, where the default settings may generate a very large k-point set.
Spin orbit coupling between the electron's spin and its orbital angular momentum couples the direction of spin with the underlying lattice. This is a relativistic effect that increases in magnitude with the nuclear charge, Z. For materials with heavy elements a scalar relativistic treatment (that is, one that neglects the spin orbit interaction) is insufficient to model the electronic band structure. In magnetic systems, the spin orbit coupling introduces a preferential direction (or set of directions) for the spin density.
The inclusion of spin orbit coupling is required for the prediction of many physical properties; for example, effective masses in semiconductors (modeling light and heavy holes); the anomalous Hall effect; Berry curvature; topological insulators, and magnetoelectrics.
In the plane waves and pseudopotential model, only the pseudized valence electrons are explicitly modeled. These electrons have a velocity, v << c, and as such the standard (non-relativistic) Kohn-Sham (KS) equations are appropriate. The spin orbit coupling is included using j-dependent pseudopotentials developed based on work by Dal Corso et al. (2005). These pseudopotentials act on KS spinor wavefunctions and an electron density with a vector spin at each grid point.
DFT can only give access to the ground state properties of a system, even if the exact exchange-correlation potential were known. For electronic excitations to be modeled Kohn-Sham equations must be substituted by the Dyson equation, where instead of the unknown exchange-correlation potential the energy dependent self energy operator is used. This operator often can be represented by the local and energy-independent exchange-correlation potential, in which case one recovers the Kohn-Sham equations for one-electron excitations. However, this approach is not appropriate for a large class of compounds, so-called correlated systems. These systems require a mixture of the Hubbard model theory and DFT. The most popular implementation is known as the DFT+U method as introduced by Anisimov and co-workers (1991).
The CASTEP implementation of DFT+U adopts a simplified, rotationally invariant approach (Cococcioni and de Gironcoli, 2005, Dudarev et al., 1998). The only external parameter needed for this approach is the effective value of the on-site Coulomb parameter, U, for each affected orbital. This parameter can be calculated theoretically (Cococcioni and de Gironcoli, 2005). However, experience shows that the best results are achieved when the U parameter is allowed to vary depending on the property of interest. CASTEP therefore does not calculate the value of U but uses it as an input parameter.
The original ideas of utilizing space group symmetry in plane-wave total energy calculations can be traced back to the k290 package (Kunc et al., 1985). The importance of this issue for achieving high performance has long been recognized. Often a high symmetry system has a fairly small unit cell. This means that the Brillouin zone is quite large and a high number of k-points are therefore required for efficient Brillouin zone sampling. This number can be greatly reduced if it is recognized that the contributions to the charge density from wavefunctions with k-vectors that are related by symmetry are related. It is then sufficient to use only one k-point from each star of symmetry-related points. Because the cost of a CASTEP calculation increases linearly with the number of k-points, any symmetry-related reduction in the number of k-points gives a direct computational speedup.
Space group symmetry is also used in CASTEP during geometry optimization. Forces on atoms, the stress tensor and consequently atomic displacements and changes in the cell parameters, are always symmetrized so that the space group symmetry can never become lower during a CASTEP calculation. However, CASTEP does not perform symmetry analysis. Instead, it uses symmetry information provided by Materials Studio.
Pseudopotentials
Plane wave basis set
Self-consistent electronic minimization
Geometry optimization
Dynamics
Mulliken population analysis
Hirshfeld charge analysis
Phonon density of states
Optical properties