Plane wave basis set
Bloch's theorem states that the electronic wavefunctions at each k-point can be expanded in terms of a discrete plane-wave basis set. In principle, an infinite number of plane waves is required for such an expansion. However, the coefficients, Ck + G, for the plane waves with small kinetic energies, |k + G|2, are more important than those with large kinetic energies. Thus, the plane wave basis set can be truncated to include only plane waves that have kinetic energies that are smaller than some particular cutoff energy as illustrated in Figure 1 (the radius of the sphere is proportional to the square root of the cutoff energy).
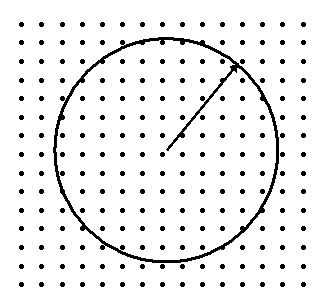
Figure 1. Schematic representation of the cutoff energy concept
Such that:
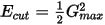
The truncation of the basis set at a finite cutoff energy will lead to an error in the computed total energy and its derivatives. It is possible to reduce the magnitude of the error in a systematic way by increasing the value of the cutoff energy. In principle, the cutoff energy should be increased until the calculated total energy converges within the required tolerance. This would be the recommended procedure if, for example, you were conducting a phase stability study where the absolute values of total energies of different structures are compared. However, the energy differences for the same structure converge at much lower cutoff energies than the total energy itself. This is due to the cancellation of errors and allows one to use moderate basis sets for reliable geometry optimization or molecular dynamics studies. These arguments are also valid for the convergence testing of Brillouin zone sampling.
Finite basis set correction
One of the difficulties associated with the use of plane-wave basis sets is that the number of basis states changes discontinuously with cutoff energy. In general these discontinuities will occur at different cutoffs for different k-points in the k-point set. In addition, at a fixed cutoff energy, a change in the size or shape of the unit cell will cause discontinuities in the plane wave basis set. This problem can be reduced by using a denser k-point set, so that the weight attached to any particular plane wave basis state is reduced. However, the problem is still present even with quite dense k-point samplings. It can be handled approximately by applying a correction factor that accounts for the difference between the number of a states in a basis set with an infinitely large number of k-points and the number of basis states actually used in the calculation (Francis and Payne, 1990).
The finite basis set correction is of the utmost importance when cell optimization is performed with a basis set that is not absolutely converged. For example, the norm-conserving silicon pseudopotential is sufficiently soft and provides accurate results with a cutoff energy for plane waves of about 200 eV. However, if one calculates the equation of state using this cutoff (that is, the volume dependence of the total energy and pressure), the volume that corresponds to the minimum in total energy does not coincide with the volume that gives zero pressure. As one repeats such EOS calculations at progressively higher cutoff energies and with better k-point sampling, the difference between the two volume values becomes smaller and smaller. In addition, the E-V curve calculated at low cutoff energy is jagged but becomes more and more smooth as the cutoff energy is increased. The reason for the jagged appearance of the E-V curve is the discontinuous change in the number of plane waves used at the same cutoff energy but for different lattice constants. The finite basis set correction, when added to the total energy, allows one to perform calculations with a fixed number of basis states and to interpolate the results as if the more physical condition of a fixed energy cutoff were used. A detailed description of the recommended use of this technique can be found in Milman et al. (1994).
The only parameter that must be known in order for this correction term to be evaluated is dEtot/d lnEcut, where Etot is the total energy of the system and Ecut is the cutoff energy. CASTEP can calculate this term automatically or you can input this parameter manually.
The value of the dEtot/d lnEcut gives a good indication of the convergence of the calculation with respect to the energy cutoff and k-point sampling. When its value per atom (that is, the value reported in the CASTEP output file divided by the number of atoms) is smaller than 0.01 eV/atom, the calculation can be considered very well converged. A value of 0.1 eV/atom is sufficient for most calculations.