Mulliken population analysis

CASTEP can perform Mulliken charges and bond populations calculations according to the formalism described by Segall et al. (1996a and 1996b).

Introduction

A disadvantage of the use of a plane wave (PW) basis set is that, because of the delocalized nature of the basis states, it provides no information regarding the localization of the electrons in the system. In contrast, a Linear Combination of Atomic Orbitals (LCAO) basis set provides a natural way of specifying quantities such as atomic charge, bond population, charge transfer, and so on.

CASTEP performs population analysis using a projection of the PW states onto a localized basis using a technique described by Sanchez-Portal et al. (1995). Population analysis of the resulting projected states uses the Mulliken formalism (Mulliken, 1955). This technique is widely used in the analysis of electronic structure calculations performed with LCAO basis sets.

Formalism

The eigenstates |ψ_α(k)>, obtained from the PW calculation when sampling at a given wavevector k, are projected onto Bloch functions formed from an LCAO basis set |ϕ_μ(k)>. In general, such a localized basis set is neither orthonormal nor complete. Therefore, care must be taken when performing the projection.

The overlap matrix of the localized basis set, S(k), is defined as:

Eq. CASTEP 63

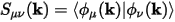
The quality of the projection can be assessed by calculating a spilling parameter:

Eq. CASTEP 64

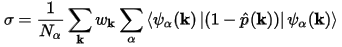
Where:

N_α is the number of PW states.
w_k are the weights associated with the calculated k-points in the Brillouin zone.
p(k) is the projection operator of Bloch functions with wavevector k generated by the atomic basis set:

Eq. CASTEP 65

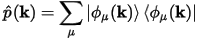
Where |ϕ_μ(k)> are the duals of the LCAO basis, such that:

Eq. CASTEP 66

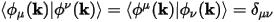
The spilling parameter varies between one, when the LCAO basis is orthogonal to the PW states, and zero, when the projected wavefunctions perfectly represent the PW states.

The density operator may be defined:

Eq. CASTEP 67

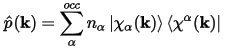
Where:
n_α are the occupancies of the PW states.
|χ_α(k)> are the projected PW states p(k)|ψ_α(k)>.
|χ^α(k)> are the duals of these states.

From this operator, you can calculated the density matrix for the atomic states as follows:

Eq. CASTEP 68

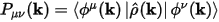
The density matrix P(k) and the overlap matrix S(k) are sufficient to perform population analysis of the electronic distribution. In Mulliken analysis (Mulliken, 1955) the charge associated with a given atom, A, is determined by:

Eq. CASTEP 69

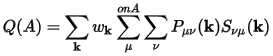
The overlap population between two atoms, A and B, is:

Eq. CASTEP 70

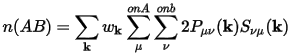
The weight of a band on a given orbital can be calculated by projecting the band onto the selected orbital. So, the weight of band α on orbital μ is given by:

Eq. CASTEP 71

The contribution of each band α to the density of states is multiplied by the weight W_αμ(k) to get the projected density of states for orbital μ.

LCAO Basis Set

In this case, the natural choice of basis set is that of pseudo-atomic orbitals, generated from the pseudopotentials used in the electronic structure calculation. These are generated automatically during population analysis. The orbitals are calculated by solving for the lowest energy eigenstates of the pseudopotential in a sphere, using a spherical Bessel basis set.

By default, the basis set used on an atom of a given species is that of the orbitals in the closed valence shell of that species. This is usually a sufficiently good basis set for population analysis and partial density of states projection. If the spilling parameter indicates that the basis set does not represent the PW states with sufficient accuracy, the number of orbitals in the atomic basis set can be increased. A spilling parameter in the region of a few percent or less is sufficiently good for population analysis and partial density of states projection. Take care when increasing the basis set dramatically, as this can lead to artificial transfers of charge.

Implementation details

The elements of the overlap matrix S(k) are computed in reciprocal space, as the imposition of periodic boundary conditions implies that the orbitals need only be evaluated on a discrete reciprocal space grid. The overlaps between orbitals on different atomic sites are calculated on the same grid with the application of a phase factor.

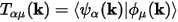
The duals of the orbitals are constructed as follows:

Eq. CASTEP 73

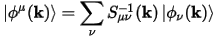
The duals of the projected wavefunctions are generated in a similar manner:

Eq. CASTEP 74

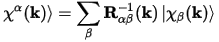
Where R(k) is the overlap matrix between projected states:

Eq. CASTEP 75

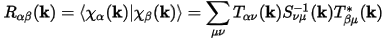
Two auxiliary matrices can be defined for efficiency, namely:

Eq. CASTEP 76

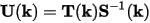
Eq. CASTEP 77

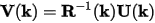
These matrices are used to calculate the spilling parameter:

Eq. CASTEP 78

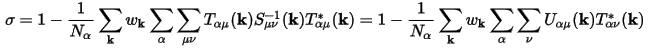
Similarly, the density matrix can be straightforwardly calculated as:

Eq. CASTEP 79

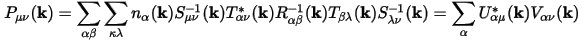
For spin dependent systems, the populations of the two spin components are calculated separately and the sum and difference of the atomic and overlap populations are calculated to find the net charge and spin, respectively.

Interpreting the results

It is widely accepted that the absolute magnitude of the atomic charges yielded by population analysis have little physical meaning. Tthey display a high degree of sensitivity to the atomic basis set with which they were calculated (Davidson and Chakravorty, 1992). However, consideration of their relative values can yield useful information (Segall et al., 1996a; Segall et al., 1996b; Winkler et al., 2001), provided that you use a consistent basis set for their calculation.

The spilling parameter should be in the region of a few percent or less to ensure that the results are reliable. If this is not the case, the number of orbitals in the basis set should be increased with care. If this does not significantly improve the spilling parameter, it may be that atomic orbitals do not provide a good representation of some of the states in the system.

Normally CASTEP reports a "charge spilling parameter", obtained from summation of σ (see Eq CASTEP 78) over all occupied bands. Additionally, CASTEP can calculate an "all bands spilling parameter", obtained from the sum over all bands, including unoccupied states. Its value is typically higher and it describes the accuracy of the representation of conduction states through LCAO-type functions.

In addition to providing an objective criterion for bonding between atoms, the overlap population can be used to assess the covalent or ionic nature of a bond. A high value of the bond population indicates a covalent bond, while a low value indicates an ionic interaction. You can obtain a further measure of ionic character from the effective ionic valence, defined as the difference between the formal ionic and Mulliken charges on the anion species. A value of zero indicates a perfectly ionic bond, while values greater than zero indicate increasing levels of covalency. See Segall et al. (1996b) for more details.

Take care when interpreting the bond order values for small unit cells. The results are incorrect whenever an atom is bonded to a number of periodic images of itself. For example, bond orders for the primitive cell of silicon are reported as 3.0, while the same calculation for the conventional cell gives 0.75. The factor of four appears because CASTEP sums the bond orders for the four bonds that link the Si atom at the origin its periodic images, in the primitive cell. A manual analysis of the multiplicities is required in such cases, specifically: determine the number of bonds to periodic images of the same atom and divide the bond order by that number.

The physical meaning of Mulliken charges or bond populations for metallic systems is unclear. This calculation is allowed, but the scientific interpretation of the results is left to the user.