Pseudopotentials

The concept of a pseudopotential is a crucial one for plane-wave total energy methods since the alternative full Coulomb potential of the electron-ion interaction decays too slowly to be accurately represented by a small number of Fourier components.

Another way of looking at the problem is to analyze wavefunctions. Consider a solid as a collection of valence electrons and ion cores. The ion cores contain nuclei and tightly bound core electrons. The valence-electron wavefunctions are orthogonal to core-electron wavefunctions. All-electron DFT methods treat core and valence electrons on an equal footing. In the pseudopotential approach ion cores are considered to be frozen. This means that properties of molecules or solids are calculated on the assumption that the ion cores are not involved in chemical bonding and do not change as a result of structural modifications.

All-electron wavefunctions of valence electrons exhibit rapid oscillations in the core region in order to satisfy the orthogonality constraint. It is impractical to represent such functions using plane waves as the size of the basis set would be prohibitive. The pseudopotential approximation replaces core electrons and the strong Coulomb potential by a weaker pseudopotential that acts on a set of pseudo wavefunctions. This potential can be represented with only a small number of Fourier coefficients. Pseudo wavefunctions ideally should have no nodes inside the core regions and thus they only require a small basis set. It is now well known that the combination of the power of plane wave technology and the pseudopotential concept is extremely useful for the description of chemical bonding (for a review see Srivastava and Weaire, 1987).

Traditionally, pseudopotentials are constructed so as to reproduce faithfully the scattering properties of the full ionic potential. The phase shift produced by the ionic core is different for each angular momentum component (s, p, d, and so on) of the valence wavefunction. Thus, the scattering from the pseudopotential must be angular momentum dependent. The most general form for a pseudopotential is:

Eq. CASTEP 4

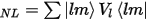
where |lm> are the spherical harmonics and V_l is the pseudopotential for angular momentum l. A pseudopotential that uses the same potential in each angular momentum channel is called a local pseudopotential. Local pseudopotentials are computationally much more efficient than a nonlocal ones, however, only a few elements can be described accurately using local pseudopotentials.

An important concept in the pseudopotential applications is the degree of hardness of a pseudopotential. A pseudopotential is considered soft when it requires a small number of Fourier components for its accurate representation and hard otherwise. Early development of accurate norm-conserving pseudopotentials quickly showed that the potentials for transition metals and for first row elements (O, C, N, and so on) turn out to be extremely hard (Bachelet et al., 1982; Kerker, 1980 ). Various schemes have been suggested to improve convergence properties of norm-conserving pseudopotentials (Troullier and Martins, 1991). Norm-conserving potentials in CASTEP are generated using the kinetic energy optimization scheme developed by Lin et al., (1993) and Lee (1996).

A more radical approach was suggested by Vanderbilt (1990), which involves relaxing the norm conservation requirement in order to generate much softer pseudopotentials. In the ultrasoft pseudopotential scheme the pseudo-wavefunctions are allowed to be as soft as possible within the core region, so that the cutoff energy can be reduced dramatically. Ultrasoft potentials (USP) have another advantage besides being much softer than the norm-conserving potentials. The generation algorithm guarantees good scattering properties over a pre-specified energy range, which results in much better transferability and accuracy of the pseudopotentials. USP usually also treats shallow core states as valences by including multiple sets of occupied states in each angular momentum channel. This also adds to high accuracy and transferability of the potentials, although at a price of computational efficiency.

Transferability is the main benefit of the pseudopotential technique over all electron DFT implementations. Pseudopotentials are constructed from a fixed electronic configuration of an isolated atom or ion and thus they reproduce the scattering properties of a nucleus in that particular configuration. They can also be used reliably for any other atomic configuration or in various solid-state environments due to the way in which they are generated, which guarantees the correct scattering properties over a wide energy range. An example of the accuracy that can be achieved across a number of structures and chemical environments is given by Milman et al. (2000).

Nonlocal pseudopotentials, even in their most efficient separable representation (Kleinman and Bylander, 1982), still consume a large share of the computational time in pseudopotential total-energy calculations. In addition, the cost of applying nonlocal pseudopotentials in reciprocal space increases with the cube of the number of atoms. Therefore, it becomes one of the dominant operations for large systems. The nonlocality of the pseudopotential, however, extends only over the region occupied by the core of the atom. As the core region is relatively small, especially if the system has a lot of vacuum in it (slab calculations, open zeolite systems, and so on), it is more efficient in this case to apply the pseudopotential in real space. The computational cost of this method increases with the square of the number of atoms and so is preferable for big systems. CASTEP uses the scheme developed originally for norm-conserving potentials (King-Smith et al., 1991 ) and was subsequently generalized for the case of ultrasoft pseudopotentials.

The separation of electrons into core and valence creates a problem when treating exchange-correlation interactions. Within the core region of the nucleus the densities of the two subsystems overlap which makes it difficult to cleanly descreen the pseudopotential during its generation. The only term in the potential energy operator that is nonlinear with respect to the electron density is the exchange-correlation energy. It has been shown by Louie et al. (1982) that there is a simple explicit scheme for treating the nonlinear exchange and correlation interaction between the core and the valence charge densities. This approach leads to significant improvements in the transferability of the potential. In particular, the spin-polarized calculations become noticeably more accurate. The nonlinear core correction (NLCC) term is especially important when semicore states are not explicitly treated as valences. On the other hand, their explicit inclusion into the valence subsystem essentially removes the need for the NLCC treatment.

Pseudopotentials

See Also: