



Next: 8. Relating linear-scaling and
Up: 7. Computational implementation
Previous: 7.6 Tensor properties of
Contents
Subsections
In this section we outline a number of details concerning the implementation
of the penalty method. These concern the derivatives of the functional
with respect to the expansion coefficients for the support functions
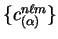 , the imposition of the
normalisation constraint and the general outline of the scheme.
, the imposition of the
normalisation constraint and the general outline of the scheme.
The support functions are expanded in spherical-wave basis functions:
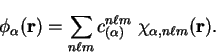 |
(7.71) |
For a functional of the support functions
![$f[\{ \phi_{\alpha} \}]$](img1075.gif) , the
derivative with respect to the expansion coefficients is
, the
derivative with respect to the expansion coefficients is
For example, for the derivative of the total energy,
![\begin{displaymath}
\frac{\delta E[\rho]}{\delta \phi_{\alpha}({\bf r})} =
4 K^{\alpha \beta} {\hat H} \phi_{\beta}({\bf r}) ,
\end{displaymath}](img1080.gif) |
(7.73) |
we obtain
in which
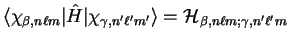 denotes the matrix element of the Kohn-Sham
Hamiltonian with respect to the spherical-wave basis functions.
denotes the matrix element of the Kohn-Sham
Hamiltonian with respect to the spherical-wave basis functions.
7.7.2 Normalisation constraint
We choose to minimise the total functional whilst constraining the
normalisation of the density-matrix to the correct value. This is
achieved firstly by projecting all gradients to be perpendicular to the
gradient of the electron number, thus maintaining the electron number to
first order, and secondly by re-converging the electron number to its
correct value before each evaluation of the total functional.
In section 7.3 the electron number gradient with respect to
the density-kernel, which is here denoted  , is given as
, is given as
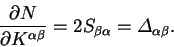 |
(7.75) |
The density-kernel along this search direction 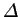 is
parameterised by
is
parameterised by 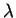 as
as
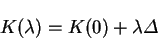 |
(7.76) |
where 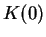 denotes the initial density-matrix.
The electron number, given by
denotes the initial density-matrix.
The electron number, given by
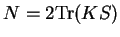 thus behaves linearly:
thus behaves linearly:
and it is a trivial matter to calculate the required value of 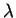 to return the electron number to its correct value.
to return the electron number to its correct value.
In general during the minimisation, the search direction is
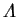 , and again this search can be parameterised by a single
parameter
, and again this search can be parameterised by a single
parameter 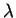 :
:
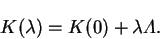 |
(7.78) |
We wish to project out from 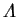 that component which is
parallel to
that component which is
parallel to 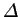 . The modified search direction
. The modified search direction
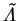 can be written as
can be written as
 |
(7.79) |
The variation of the electron number along this modified direction is
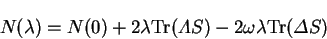 |
(7.80) |
and we wish the coefficient of the linear term in 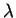 to vanish,
which defines the required value of
to vanish,
which defines the required value of 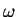 to be
to be
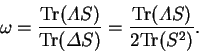 |
(7.81) |
Since the electron number depends linearly upon the density-kernel,
after this projection, the electron number is constant along the modified
search direction, and the electron number need not be corrected after
a trial step is taken.
The electron number gradient with respect to the support functions
is given in section 7.3 and denoted by
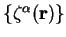 :
:
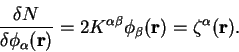 |
(7.82) |
The support function variation is again parameterised by the parameter
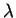 :
:
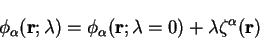 |
(7.83) |
and this results in the following quadratic variation of the overlap matrix
which defines the matrices 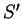 and
and 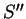 . The variation of the electron
number is therefore also quadratic
. The variation of the electron
number is therefore also quadratic
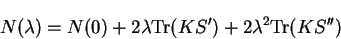 |
(7.85) |
and the roots of this expression can be found to correct the electron number.
We consider a general search direction for the localised functions denoted
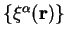 and modify this search direction to obtain the
direction which maintains the electron number to first order:
and modify this search direction to obtain the
direction which maintains the electron number to first order:
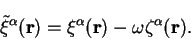 |
(7.86) |
Now varying the localised functions according to
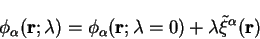 |
(7.87) |
results in the following variation of the electron number:
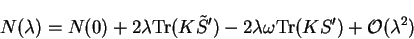 |
(7.88) |
where
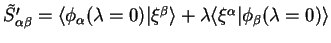 .
Thus to maintain the electron number to first order, we choose
.
Thus to maintain the electron number to first order, we choose
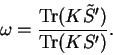 |
(7.89) |
In this case, the electron number is not constant along the search direction,
but will still vary quadratically, so that it is necessary to correct the
density-matrix before evaluating the total functional.
The initialisation of the density-matrix is described in chapter 8.
The functional minimisation consists of two nested loops. The inner loop
consists of the minimisation with respect to the density-kernel, while
keeping the support functions constant. As shown in section
7.4, this corresponds to making the density-matrix commute
with the Hamiltonian in the representation of the current support
functions. The outer loop consists of the support function minimisations,
which in section 7.4 were shown to correspond to solving the
Kohn-Sham equations. In general, we find that two or three cycles of the
inner loop for each cycle of the outer loop suffice, and this is demonstrated
in figure 7.1 in which three cycles of the inner loop appears
to give the best performance to computational cost ratio.
Figure 7.1:
Rate of convergence for different numbers of inner cycles. In the legend,
 corresponds to
corresponds to  cycles of the inner loop for each
iteration of the outer loop (horizontal axis).
cycles of the inner loop for each
iteration of the outer loop (horizontal axis).
|
|
The conjugate
gradients scheme is used to determine the search directions from the
gradients, and these gradients are then projected perpendicular to the
electron number gradient as described in section 7.7.2.
We approximate the total functional by a parabola along the search
direction, using the initial value of the functional, the first derivative
of the functional at the initial position (which is simply the scalar
product of the steepest descent and search directions) and the value of the
functional at some trial position. The value of the functional at the
predicted minimum is then evaluated. If this value deviates significantly
from the value predicted by the quadratic fit, a cubic fit is constructed
using this new value of the functional. In general, this is only
necessary for the first few steps, and the parabolic fit is very good.
In the case of the support function variation, the support functions are
altered to give the correct number of electrons before each evaluation of the
functional. The conjugate gradients procedure is reset after a finite
number of steps, and this is illustrated in figure 7.2 for the
inner and outer loops. In both cases,
we see that there is little advantage in conjugating more than eight
gradients before resetting.
Figure 7.2:
Performance of the conjugate gradients algorithm in the density-kernel
variation (left) and the support function variation (right).
|
|
Once the functional has been minimised, the correction to the total energy
is calculated. The whole calculation is generally repeated for a few different
values of  to ensure that the corrected energy has indeed
converged.
to ensure that the corrected energy has indeed
converged.




Next: 8. Relating linear-scaling and
Up: 7. Computational implementation
Previous: 7.6 Tensor properties of
Contents
Peter Haynes
![]() , the imposition of the
normalisation constraint and the general outline of the scheme.
, the imposition of the
normalisation constraint and the general outline of the scheme.
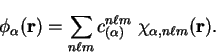
![$\displaystyle \frac{\partial f[\{ \phi_{\alpha} \}]}{\partial c^{n \ell m}_{(\beta)}}$](img1076.gif)
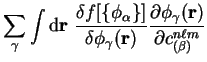
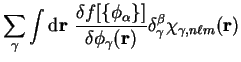
![$\displaystyle \int {\mathrm d}{\bf r}~\frac{\delta f[ \{ \phi_{\alpha} \} ]}
{\delta \phi_{\beta}({\bf r})}
\chi_{\beta , n \ell m}({\bf r}) .$](img1079.gif)
![\begin{displaymath}
\frac{\delta E[\rho]}{\delta \phi_{\alpha}({\bf r})} =
4 K^{\alpha \beta} {\hat H} \phi_{\beta}({\bf r}) ,
\end{displaymath}](img1080.gif)
![$\displaystyle \frac{\partial E[\rho]}{\partial c^{n \ell m}_{(\beta)}}$](img1081.gif)
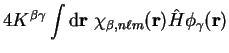
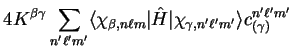
![]() , is given as
, is given as
![]() , and again this search can be parameterised by a single
parameter
, and again this search can be parameterised by a single
parameter ![]() :
:
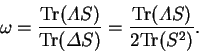
![]() :
:
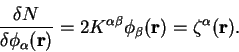
![]() and modify this search direction to obtain the
direction which maintains the electron number to first order:
and modify this search direction to obtain the
direction which maintains the electron number to first order:
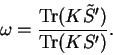
![\includegraphics [width=12cm]{ndmits.eps}](img1115.gif)
![\includegraphics [width=16cm]{cgits.eps}](img1117.gif)
![]() to ensure that the corrected energy has indeed
converged.
to ensure that the corrected energy has indeed
converged.