



Next: 7.5 Occupation number preconditioning
Up: 7. Computational implementation
Previous: 7.3 Penalty functional and
Contents
7.4 Physical interpretation
At this stage we examine the energy gradients derived in section
7.2. At the minimum of the total functional
![$Q[\rho;\alpha]$](img1000.gif) ,
,
![\begin{displaymath}
\frac{\partial Q[\rho;\alpha]}{\partial K^{\alpha \beta}} = ...
...a} + 2 \alpha \left[ SKS(1-KS)(1-2KS) \right]_{\beta
\alpha} .
\end{displaymath}](img1001.gif) |
(7.44) |
Making the Löwdin transformation of this gradient into the representation
of a set of orthonormal
orbitals (using the results of section 4.6) yields
![\begin{displaymath}
2 S^{1 \over 2} \left[ {\tilde H} + \alpha {\tilde K} (1 - {\tilde K})
(1 - 2 {\tilde K}) \right] S^{1 \over 2} = 0
\end{displaymath}](img1002.gif) |
(7.45) |
which (pre- and post-multiplying by
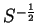 ) simplifies to
) simplifies to
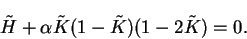 |
(7.46) |
This result shows that at the minimum, 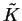 and
and 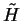 can be
diagonalised simultaneously, and will therefore commute. The result of
the variation of the density-kernel is to make the density-matrix commute
with the Hamiltonian in the representation of the current support functions.
Transforming to the diagonal frame by making a
unitary transformation (the eigenvalues of
can be
diagonalised simultaneously, and will therefore commute. The result of
the variation of the density-kernel is to make the density-matrix commute
with the Hamiltonian in the representation of the current support functions.
Transforming to the diagonal frame by making a
unitary transformation (the eigenvalues of 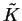 being
being 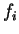 and
those of
and
those of 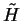 being
being 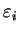 ) we obtain the following
relationship:
) we obtain the following
relationship:
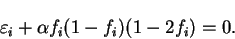 |
(7.47) |
For the derivative with respect to the support functions we have
![\begin{displaymath}
\frac{\delta Q[\rho;\alpha]}{\partial \phi_{\alpha}({\bf r})...
...K(1-SK)(1-2SK)]^{\alpha \beta}
\right\} \phi_{\beta}({\bf r})
\end{displaymath}](img1005.gif) |
(7.48) |
which can again be transformed first into an orthonormal representation
defined by the Löwdin transformation:
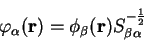 |
(7.49) |
to obtain
Assuming that we have performed the minimisation with respect to the
density-kernel for the current support functions, transforming to the
representation which simultaneously
diagonalises the Hamiltonian and density-matrix, by the unitary
transformation
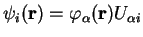 ,
yields
,
yields
which is a Kohn-Sham-like equation, but where the energy eigenvalue
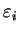 does not explicitly appear since no orthonormalisation
constraint is explicitly applied. Using equation 7.47, however,
yields
does not explicitly appear since no orthonormalisation
constraint is explicitly applied. Using equation 7.47, however,
yields
![\begin{displaymath}
\frac{\delta Q[\rho;\alpha]}{\delta \psi_i({\bf r})} = 0 =
4 f_i \left[ {\hat H} - \varepsilon_i \right]\psi_i({\bf r})
\end{displaymath}](img1016.gif) |
(7.52) |
and so, at least for 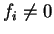 , we see that the support function
variations are equivalent to making the related wave-functions obey the
Kohn-Sham equations.
The factor of
, we see that the support function
variations are equivalent to making the related wave-functions obey the
Kohn-Sham equations.
The factor of 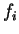 will slow this convergence for unoccupied bands, since
for
will slow this convergence for unoccupied bands, since
for 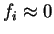 the gradient is small. In the next section (7.5) we therefore turn our attention to a potential method for eliminating this
problem.
the gradient is small. In the next section (7.5) we therefore turn our attention to a potential method for eliminating this
problem.




Next: 7.5 Occupation number preconditioning
Up: 7. Computational implementation
Previous: 7.3 Penalty functional and
Contents
Peter Haynes
![]() ,
,
![\begin{displaymath}
\frac{\delta Q[\rho;\alpha]}{\partial \phi_{\alpha}({\bf r})...
...K(1-SK)(1-2SK)]^{\alpha \beta}
\right\} \phi_{\beta}({\bf r})
\end{displaymath}](img1005.gif)
![$\displaystyle \frac{\delta Q[\rho;\alpha]}{\delta \varphi_{\alpha}({\bf r})}$](img1007.gif)
![$\displaystyle \int {\mathrm d}{\bf r'}~ \frac{\delta Q[\rho;\alpha]}{\delta \ph...
... \beta}^{1 \over 2} \frac{\delta Q[\rho;\alpha]}
{\delta \phi_{\beta}({\bf r})}$](img1008.gif)
![$\displaystyle 4 S_{\alpha i}^{1 \over 2} K^{ij} \left[ {\hat H}
+ \alpha SK(1-SK)(1-2SK) \right]_j^k S_{kl}^{1 \over 2} \varphi_l({\bf r})$](img1009.gif)
![$\displaystyle \frac{\delta Q[\rho;\alpha]}{\delta \psi_i({\bf r})}$](img1012.gif)
![$\displaystyle U_{i \alpha}^{\dag } \frac{\delta Q[\rho;\alpha]}{\delta \varphi_{\alpha}({\bf r})}$](img1013.gif)