Next: 7.1 Total energy and
Up: thesis
Previous: 6.2 Corrected penalty functional
Contents
7. Computational implementation
In this chapter we describe how the corrected penalty functional method
described in section 6.2 has been implemented in a total
energy computer code to perform linear-scaling quantum-mechanical
calculations on arbitrary systems.
As mentioned in section 4.6, the density-matrix is
represented in the form
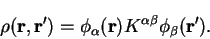 |
(7.1) |
We refer to the contravariant quantity
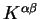 as the
density-kernel, and the covariant quantities
as the
density-kernel, and the covariant quantities
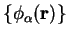 are localised non-orthogonal support functions, which are themselves
expanded in terms of the spherical-wave basis-set of chapter 5:
are localised non-orthogonal support functions, which are themselves
expanded in terms of the spherical-wave basis-set of chapter 5:
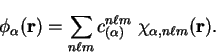 |
(7.2) |
We now proceed to express the total energy and penalty functional in
terms of these quantities, and also to calculate gradients with respect
to the density-kernel and expansion coefficients
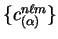 .
We will also discuss the implementation of the normalisation constraint and
also how the convergence might be improved by the use of a preconditioning scheme for
the gradients.
.
We will also discuss the implementation of the normalisation constraint and
also how the convergence might be improved by the use of a preconditioning scheme for
the gradients.
Subsections




Next: 7.1 Total energy and
Up: thesis
Previous: 6.2 Corrected penalty functional
Contents
Peter Haynes