



Next: 7.7 Practical details
Up: 7. Computational implementation
Previous: 7.5 Occupation number preconditioning
Contents
7.6 Tensor properties of the gradients
We have already noted that it is important to take note of the tensor
properties of quantities when non-orthogonal functions are involved.
In particular, the gradient of the scalar functional with respect to
the contravariant density-kernel is a covariant quantity which should not
be directly added to the contravariant density-kernel, but should first be
converted into contravariant form using the metric tensor
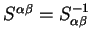 .
Thus the correct search direction for the density-kernel variation
is
.
Thus the correct search direction for the density-kernel variation
is
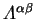 given by
given by
While the penalty functional derivative is simplified, the energy derivative
picks up two factors of the inverse overlap matrix, which, as in the case of
occupation number preconditioning, makes this difficult to implement. Neglecting this
conversion of the covariant gradient to its contravariant form corresponds to
approximating the overlap matrix by the identity. Thus the covariant gradient
corresponds to taking the first term only in the series expansion of the
overlap matrix inverse in equation 7.66. Again, neglect of this
correction may lead to a deterioration in the efficiency of the minimisation
procedure as the system-size increases.
We now consider the contravariant gradient of the functional with respect to
the covariant support functions. This is a first-rank tensor quantity
whereas the density-kernel gradient is a second-rank tensor.
The correct covariant gradient is thus
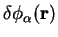 given by
given by
The covariant preconditioned gradient in particular turns out to be
![\begin{displaymath}
\delta \phi_{\alpha} ({\bf r}) = 4 \left\{ {\hat H} \delta_{...
...1-2SK)\right]_{\alpha}^{~\beta} \right\}
\phi_{\beta}({\bf r})
\end{displaymath}](img1074.gif) |
(7.70) |
so that the factor of the inverse overlap matrix is now eliminated.




Next: 7.7 Practical details
Up: 7. Computational implementation
Previous: 7.5 Occupation number preconditioning
Contents
Peter Haynes
![]() .
Thus the correct search direction for the density-kernel variation
is
.
Thus the correct search direction for the density-kernel variation
is
![]() given by
given by
![$\displaystyle S^{\alpha i} \frac{\partial Q[\rho;\alpha]}
{\partial K^{ji}} S^{j \beta}$](img1066.gif)
![]() given by
given by
![$\displaystyle S_{\alpha \beta}
\frac{\delta Q[\rho;\alpha]}{\delta \phi_{\beta}({\bf r})}$](img1071.gif)