



Next: 6.2 Corrected penalty functional
Up: 6. Penalty Functionals
Previous: 6. Penalty Functionals
Contents
Subsections
6.1 Kohn's method
As mentioned in section 4.4.3, Kohn [135] has
suggested the use of a penalty functional to impose the idempotency
condition, and has proved a variational principle based upon it.
We consider trial density-matrices
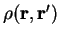 expressed in diagonal form with real orthonormal extended orbitals
expressed in diagonal form with real orthonormal extended orbitals
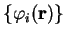 and occupation numbers
and occupation numbers
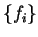 :
:
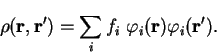 |
(6.1) |
The functional
![${\cal Q}[{\rho};\mu,\alpha]$](img795.gif) is then formed:
is then formed:
![\begin{displaymath}
{\cal Q}[{\rho};\mu,\alpha] \equiv E_{\mathrm{NI}}[{\rho}^2] -
\mu N[{\rho}^2] + \alpha {\cal P}[{\rho}]
\end{displaymath}](img796.gif) |
(6.2) |
in which
and where 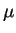 is the chemical potential and
is the chemical potential and  is a positive real
parameter.
is a positive real
parameter.
Kohn proves the following variational principle: that for some
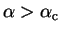 , the minimum value of
, the minimum value of
![${\cal Q}[{\rho};\mu,\alpha]$](img795.gif) is obtained for the idempotent ground-state
density-matrix
is obtained for the idempotent ground-state
density-matrix 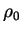 and that the minimum value is the ground-state grand potential i.e.
and that the minimum value is the ground-state grand potential i.e.
![\begin{displaymath}
\mathop{\rm min}\limits _{\rho} {\cal Q}[{\rho};\mu,\alpha] ...
...m_{i,\varepsilon^{(0)}_i \leq \mu} (\varepsilon^{(0)}_i - \mu)
\end{displaymath}](img806.gif) |
(6.6) |
in which the
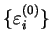 are the exact eigenvalues of the
self-consistent Hamiltonian, generated by the ground-state density-matrix
are the exact eigenvalues of the
self-consistent Hamiltonian, generated by the ground-state density-matrix
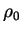 .
.
The critical value of  , denoted
, denoted
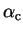 , is given by
, is given by
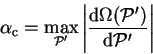 |
(6.7) |
in which
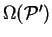 is the conditional minimum defined by
is the conditional minimum defined by
![\begin{displaymath}
\Omega({\cal P}') = \mathop{\rm min}\limits _{{\cal P}[{\rho...
...}'} \left( E_{\mathrm{NI}}[{\rho}^2]
- \mu N[{\rho}^2] \right)
\end{displaymath}](img811.gif) |
(6.8) |
i.e. the minimum grand potential for all trial density-matrices which give
a penalty functional value of 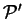 . Clearly
. Clearly
![\begin{displaymath}
\alpha_{\mathrm c} \geq \left\vert \frac{{\mathrm d} \Omega(...
..._i \leq \mu}
(\varepsilon^{(0)}_i - \mu)^2 \right]^{1 \over 2}
\end{displaymath}](img813.gif) |
(6.9) |
although this is only a lower bound on
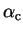 .
.
Figure 6.1:
Behaviour of Kohn's penalty functional
![${\cal P}[\rho]$](img815.gif) when a single occupation number
when a single occupation number 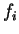 is varied and all others
are zero or unity.
is varied and all others
are zero or unity.
|
|
Kohn's variational principle is based on the non-interacting energy
![$E_{\mathrm{NI}}[\rho^2]$](img817.gif) . We now present a simple modification of this functional
based upon
self-consistent variation of the interacting energy. Consider the
functional
. We now present a simple modification of this functional
based upon
self-consistent variation of the interacting energy. Consider the
functional
![\begin{displaymath}
{\tilde {\cal Q}}[{\rho};\mu,\alpha] = E[{\rho}] - \mu N[{\rho}]
+ \alpha {\cal P}[{\rho}]
\end{displaymath}](img818.gif) |
(6.10) |
in which ![$E[{\rho}]$](img819.gif) is the interacting energy, and
is the interacting energy, and 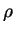 is
a positive semi-definite trial density-matrix. A given set of occupation
numbers
is
a positive semi-definite trial density-matrix. A given set of occupation
numbers 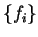 fixes the value of the penalty functional
fixes the value of the penalty functional
![${\cal P}[{\rho}]$](img821.gif) and variation
of
and variation
of
![${\tilde {\cal Q}}[{\rho};\mu,\alpha]$](img822.gif) with respect to the orbitals
with respect to the orbitals
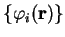 at fixed occupation numbers and subject to the
orthonormality constraint yields Kohn-Sham-like equations. Self-consistent
variation of the occupation numbers
at fixed occupation numbers and subject to the
orthonormality constraint yields Kohn-Sham-like equations. Self-consistent
variation of the occupation numbers 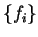 (i.e. allowing the
orbitals to relax, as in section 4.2) yields
(i.e. allowing the
orbitals to relax, as in section 4.2) yields
![\begin{displaymath}
\frac{\partial {\tilde {\cal Q}}[{\rho};\mu,\alpha]}{\partia...
... + \frac{\alpha}{{\cal P}[{\rho}]}
f_i (1 - f_i) (1 - 2 f_i) .
\end{displaymath}](img824.gif) |
(6.11) |
In the case of idempotent density-matrices,
for which
![${\cal P}[{\rho}]=0$](img825.gif) , we obtain the special cases
, we obtain the special cases
![\begin{displaymath}
\left.\frac{\partial {\tilde Q}[{\rho};\mu,\alpha]}
{\partia...
..._i=(0^{\pm},1^{\pm})} = 2 ({\varepsilon}_i - \mu)
\pm \alpha .
\end{displaymath}](img826.gif) |
(6.12) |
For this functional the critical value of  , again denoted
, again denoted
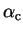 , is
given by
, is
given by
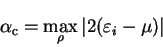 |
(6.13) |
where the maximum is strictly over those density-matrices searched during the
minimisation.
For
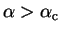 the total functional
the total functional
![${\tilde {\cal Q}}[{\rho};\mu,\alpha]$](img822.gif) takes its minimum value when
takes its minimum value when
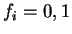 for
for
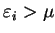 and
and
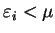 respectively. In particular, for the
ground-state density-matrix
respectively. In particular, for the
ground-state density-matrix  , the functional is strictly increasing
with respect to all variations in occupation numbers. The discontinuity in
the occupation number derivative of the penalty functional at idempotency is
required because of the non-variational behaviour of the total energy
with respect to these variations (section 4.2).
The behaviour of the penalty functional for unconstrained occupation
number variation is plotted in figure 6.1, and in figure
6.2 the total functional is sketched schematically for
several representative values of the parameter
, the functional is strictly increasing
with respect to all variations in occupation numbers. The discontinuity in
the occupation number derivative of the penalty functional at idempotency is
required because of the non-variational behaviour of the total energy
with respect to these variations (section 4.2).
The behaviour of the penalty functional for unconstrained occupation
number variation is plotted in figure 6.1, and in figure
6.2 the total functional is sketched schematically for
several representative values of the parameter  . This demonstrates
how the minimising density-matrix is idempotent only for
. This demonstrates
how the minimising density-matrix is idempotent only for
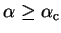 .
.
Figure 6.2:
Schematic illustration of Kohn's variational principle: behaviour of the total energy (black) and total functional (red) for representative values of  .
.
|
|
6.1.2 Implementation problems
The conjugate gradients algorithm for minimising functions is described
in appendix B. Throughout the lengthy derivation it is clear that
the useful results obtained and the remarkably simple final result are due
to the special properties of quadratic functions.
Any function may be expanded in the form of a Taylor
series about an analytic point, and around a minimum where the first order term
from the gradient vanishes, a quadratic function is generally a good
approximation. However, we note that the Kohn penalty functional has a branch
point from the square-root function exactly at the ground-state
minimum which we seek, and so the function cannot be Taylor-expanded there.
Local information from the gradient cannot be used to infer the global
shape of the function. This is illustrated in figure 6.3
for the case of a parabolic interpolation to find a line minimum based
upon the gradient and a trial step, but the problem is even worse in the
multi-dimensional space since the ``conjugate'' directions constructed from
the gradients will not point in the direction of the ground-state minimum.
Figure 6.3:
Failure of quadratic interpolation for Kohn's penalty functional.
|
|
This problem is reflected in the very poor convergence when an attempt is
made to minimise the functional using conjugate gradients: the steepest
descents method actually performs better because it does not assume global quadratic
behaviour. Also, the penalty functional does not vanish at the minimum
sufficiently quickly
as the parameter  is increased. However, the root-mean-square error in
the occupation numbers
is increased. However, the root-mean-square error in
the occupation numbers
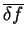 , given by
, given by
![\begin{displaymath}
\overline{\delta f} = \frac{{\cal P}[\rho]}{\sqrt{N/2}}
\end{displaymath}](img835.gif) |
(6.14) |
in fact decays more rapidly, so that the total energy calculated at the
minimum is
quite accurate, although it is neither variational nor an upper bound. Also, although the
total functional
![${\tilde {\cal Q}}[\rho;\mu,\alpha]$](img836.gif) decreases monotonically,
the total energy does not. Thus no advantage is gained by
using the variational property, since it can only be applied to the
total energy when
decreases monotonically,
the total energy does not. Thus no advantage is gained by
using the variational property, since it can only be applied to the
total energy when
![${\cal P}[\rho] = 0$](img464.gif) .
The variational property of the total functional is that it is minimal at the
ground-state, but this minimum is defined in terms of the functional taking
its minimum value there, not in terms of a vanishing gradient
(the gradient being undefined at the ground-state).
Because of the non-variational behaviour of the total energy with respect to
the occupation numbers at the ground-state, it is impossible to construct
a penalty functional which has a continuous first derivative at the
ground-state and also results in a variational principle for the total
energy.
.
The variational property of the total functional is that it is minimal at the
ground-state, but this minimum is defined in terms of the functional taking
its minimum value there, not in terms of a vanishing gradient
(the gradient being undefined at the ground-state).
Because of the non-variational behaviour of the total energy with respect to
the occupation numbers at the ground-state, it is impossible to construct
a penalty functional which has a continuous first derivative at the
ground-state and also results in a variational principle for the total
energy.
Figure 6.4:
Convergence properties of Kohn's penalty functional: behaviour of penalty functional and occupation numbers with  .
.
|
|
In figure 6.4 we present the results of tests on an 8-atom silicon cell
to demonstrate the behaviour of the functional. As the penalty functional
parameter  is increased, both the contribution of the penalty
functional to the total functional
is increased, both the contribution of the penalty
functional to the total functional
![$\alpha {\cal P}[\rho]$](img838.gif) , and the root mean
square error in the occupation numbers
, and the root mean
square error in the occupation numbers
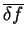 decrease, but
not rapidly enough with
decrease, but
not rapidly enough with  since the number of iterations required to
reach convergence increases with
since the number of iterations required to
reach convergence increases with  making the calculations too
expensive for practical applications. For example, the number of iterations
required to converge the
total functional to
making the calculations too
expensive for practical applications. For example, the number of iterations
required to converge the
total functional to 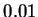 eV per atom increases by a factor of more than ten
when
eV per atom increases by a factor of more than ten
when  is increased from 100 eV to 1000 eV. Even with the smaller
value for
is increased from 100 eV to 1000 eV. Even with the smaller
value for  , the rate of convergence is much slower than traditional
methods, and this is due to the incompatibility of the functional with the
conjugate gradients scheme.
, the rate of convergence is much slower than traditional
methods, and this is due to the incompatibility of the functional with the
conjugate gradients scheme.




Next: 6.2 Corrected penalty functional
Up: 6. Penalty Functionals
Previous: 6. Penalty Functionals
Contents
Peter Haynes
![]() expressed in diagonal form with real orthonormal extended orbitals
expressed in diagonal form with real orthonormal extended orbitals
![]() and occupation numbers
and occupation numbers
![]() :
:
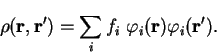
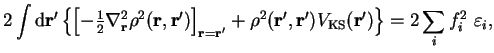
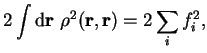
![$\displaystyle \left[ \int {\mathrm d}{\bf r}~ \left(
{\rho}^2(1 - {\rho})^2 \ri...
...r})
\right]^{1 \over 2} = \left[ \sum_i f_i^2
(1 - f_i)^2 \right]^{1 \over 2} ,$](img803.gif)
![]() , the minimum value of
, the minimum value of
![]() is obtained for the idempotent ground-state
density-matrix
is obtained for the idempotent ground-state
density-matrix ![]() and that the minimum value is the ground-state grand potential i.e.
and that the minimum value is the ground-state grand potential i.e. ![\begin{displaymath}
\mathop{\rm min}\limits _{\rho} {\cal Q}[{\rho};\mu,\alpha] ...
...m_{i,\varepsilon^{(0)}_i \leq \mu} (\varepsilon^{(0)}_i - \mu)
\end{displaymath}](img806.gif)
![]() , denoted
, denoted
![]() , is given by
, is given by
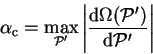
![\begin{displaymath}
\Omega({\cal P}') = \mathop{\rm min}\limits _{{\cal P}[{\rho...
...}'} \left( E_{\mathrm{NI}}[{\rho}^2]
- \mu N[{\rho}^2] \right)
\end{displaymath}](img811.gif)
![\begin{displaymath}
\alpha_{\mathrm c} \geq \left\vert \frac{{\mathrm d} \Omega(...
..._i \leq \mu}
(\varepsilon^{(0)}_i - \mu)^2 \right]^{1 \over 2}
\end{displaymath}](img813.gif)
![\begin{picture}(285,199)
\put(28,0){\includegraphics [width=8cm]{penfun.eps}}
\put(6,171){${\cal P}[\rho]$}
\put(262,6){$f_i$}
\end{picture}](img814.gif)
![]() . We now present a simple modification of this functional
based upon
self-consistent variation of the interacting energy. Consider the
functional
. We now present a simple modification of this functional
based upon
self-consistent variation of the interacting energy. Consider the
functional
![\begin{displaymath}
\frac{\partial {\tilde {\cal Q}}[{\rho};\mu,\alpha]}{\partia...
... + \frac{\alpha}{{\cal P}[{\rho}]}
f_i (1 - f_i) (1 - 2 f_i) .
\end{displaymath}](img824.gif)
![\begin{displaymath}
\left.\frac{\partial {\tilde Q}[{\rho};\mu,\alpha]}
{\partia...
..._i=(0^{\pm},1^{\pm})} = 2 ({\varepsilon}_i - \mu)
\pm \alpha .
\end{displaymath}](img826.gif)
![\includegraphics [width=13cm]{kohnfun.eps}](img832.gif)
![]() is increased. However, the root-mean-square error in
the occupation numbers
is increased. However, the root-mean-square error in
the occupation numbers
![]() , given by
, given by
![\begin{displaymath}
\overline{\delta f} = \frac{{\cal P}[\rho]}{\sqrt{N/2}}
\end{displaymath}](img835.gif)
![\begin{picture}(427,242)
\put(71,14){\includegraphics [width=10cm]{kohn.eps}}
\p...
...$\alpha {\cal P}[\rho]$\ /eV}
\put(370,142){$\overline{\delta f}$}
\end{picture}](img837.gif)
![]() is increased, both the contribution of the penalty
functional to the total functional
is increased, both the contribution of the penalty
functional to the total functional
![]() , and the root mean
square error in the occupation numbers
, and the root mean
square error in the occupation numbers
![]() decrease, but
not rapidly enough with
decrease, but
not rapidly enough with ![]() since the number of iterations required to
reach convergence increases with
since the number of iterations required to
reach convergence increases with ![]() making the calculations too
expensive for practical applications. For example, the number of iterations
required to converge the
total functional to
making the calculations too
expensive for practical applications. For example, the number of iterations
required to converge the
total functional to ![]() eV per atom increases by a factor of more than ten
when
eV per atom increases by a factor of more than ten
when ![]() is increased from 100 eV to 1000 eV. Even with the smaller
value for
is increased from 100 eV to 1000 eV. Even with the smaller
value for ![]() , the rate of convergence is much slower than traditional
methods, and this is due to the incompatibility of the functional with the
conjugate gradients scheme.
, the rate of convergence is much slower than traditional
methods, and this is due to the incompatibility of the functional with the
conjugate gradients scheme.