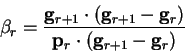Next: Bibliography
Up: thesis
Previous: A. Bessel function identities
Contents
B. Conjugate gradients
In order to find the minimum of some function 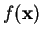 , it is of course
necessary to solve the equation
, it is of course
necessary to solve the equation
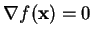 , but this is not
possible in practice. Rather,
, but this is not
possible in practice. Rather,
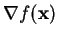 is used as a search
direction in the multi-dimensional parameter-space of vectors
is used as a search
direction in the multi-dimensional parameter-space of vectors 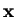 to minimise the function iteratively.
One way to do this is to move along
these directions of steepest descent, finding the minimum along
each one and then calculating a new direction from that minimum until we
find the ground-state. The minimum along a certain direction (the line
minimum) is found when the direction along which we are searching becomes
perpendicular to the gradient. Thus if we use this method
of steepest descents, consecutive search directions are always perpendicular,
and it is clear that this is inefficient since we are only
using the current steepest descent direction and throwing away all previous
knowledge which could be used to build up a more accurate picture of the
functional we are trying to minimise. In fact, the steepest descents method is
only efficient when the minimum is ``spherical'' i.e. when the eigenvalues
of the Hessian are all of the same order. If this is not the case, then the
method is very slow, and is not guaranteed to converge to the minimum in a
finite number of steps. A particularly bad case is that of the ``narrow
valley'' illustrated in figure B.1.
to minimise the function iteratively.
One way to do this is to move along
these directions of steepest descent, finding the minimum along
each one and then calculating a new direction from that minimum until we
find the ground-state. The minimum along a certain direction (the line
minimum) is found when the direction along which we are searching becomes
perpendicular to the gradient. Thus if we use this method
of steepest descents, consecutive search directions are always perpendicular,
and it is clear that this is inefficient since we are only
using the current steepest descent direction and throwing away all previous
knowledge which could be used to build up a more accurate picture of the
functional we are trying to minimise. In fact, the steepest descents method is
only efficient when the minimum is ``spherical'' i.e. when the eigenvalues
of the Hessian are all of the same order. If this is not the case, then the
method is very slow, and is not guaranteed to converge to the minimum in a
finite number of steps. A particularly bad case is that of the ``narrow
valley'' illustrated in figure B.1.
Figure B.1:
Steepest descents method - a large number of steps is required to
find the minimum.
|
|
By contrast, the method of conjugate gradients [187] takes
information from previous steps into account, but only requires that the
previous search direction (rather than all previous search directions as might
be expected) be stored. For a full description see [188].
We consider a general quadratic scalar function of a
number of variables, written as a vector 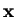 :
:
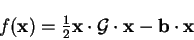 |
(B.1) |
in which 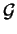 is a positive definite symmetric matrix (so that the
function has a single global minimum) and
is a positive definite symmetric matrix (so that the
function has a single global minimum) and 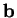 is some constant vector.
We denote the line minima (i.e. the points at which the search direction
changes) by the set of points
is some constant vector.
We denote the line minima (i.e. the points at which the search direction
changes) by the set of points
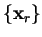 and the gradients at those
points are
and the gradients at those
points are
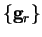
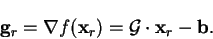 |
(B.2) |
We label the search directions
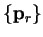 . In the steepest descents
method,
. In the steepest descents
method,
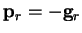 and we move along this direction an
amount described by the parameter
and we move along this direction an
amount described by the parameter 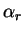 until at the end
(at
until at the end
(at 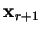 ) the search direction is perpendicular to the gradient
) the search direction is perpendicular to the gradient
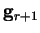 :
:
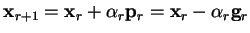 |
|
|
(B.3) |
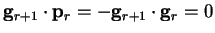 |
|
|
(B.4) |
which proves that consecutive search directions are always mutually
perpendicular in
this method. Now, for 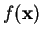 defined by equation B.1 we have
defined by equation B.1 we have
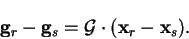 |
(B.5) |
The minimum of 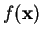 along the direction
along the direction 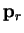 is at
is at
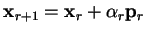 and is still given by
condition (B.4), so that
and is still given by
condition (B.4), so that 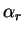 is given by
is given by
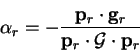 |
(B.6) |
and using (B.5) with 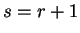 we obtain
we obtain
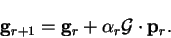 |
(B.7) |
A set of search directions
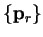 are said to be conjugate
directions (with respect to
are said to be conjugate
directions (with respect to 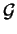 ) if they satisfy the condition
) if they satisfy the condition
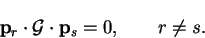 |
(B.8) |
These directions are linearly independent which can be proved by
reductio ad absurdum: assume the directions are linearly
dependent i.e. there is a set of numbers
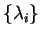 , not all vanishing,
for which
, not all vanishing,
for which
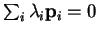 . But operating on both sides by
. But operating on both sides by
 and taking the scalar product with
and taking the scalar product with  implies
implies
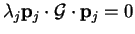 for all
for all 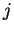 by (B.8),
and
by (B.8),
and
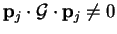 since
since 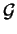 is positive
definite, and so we obtain the contradiction that
is positive
definite, and so we obtain the contradiction that 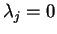 for all
for all 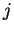 .
.
We can construct a set of these directions from a set of linearly
dependent directions
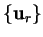 using a procedure analogous to
Gram-Schmidt orthogonalisation i.e.
using a procedure analogous to
Gram-Schmidt orthogonalisation i.e.
where
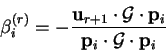 |
(B.10) |
which we prove by induction. Assuming that we have 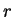 conjugate directions
obeying (B.8) and construct
conjugate directions
obeying (B.8) and construct 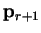 according to
(B.9) then
according to
(B.9) then
for 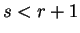 , since
, since 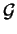 is symmetric. Now
is symmetric. Now 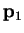 and
and 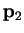 are trivially verified to
be conjugate directions and so the proof is complete.
are trivially verified to
be conjugate directions and so the proof is complete.
It follows that any other vector may be written as a combination of these
conjugate directions, in particular the vector from the initial point
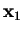 to the minimum
to the minimum
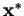 in an
in an 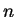 -dimensional space is
-dimensional space is
from equation B.2 and the fact that the gradient vanishes at the
minimum i.e.
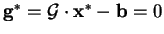 .
We note therefore that
.
We note therefore that
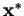 can be reached in
can be reached in 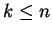 steps
from
steps
from 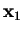 where the
where the 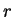 -th step is given by
-th step is given by
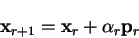 |
(B.13) |
with 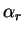 given by (B.12). Applying (B.5) to
given by (B.12). Applying (B.5) to
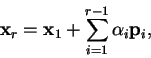 |
(B.14) |
we obtain
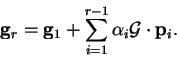 |
(B.15) |
When the scalar product with 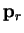 is taken this gives
is taken this gives
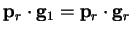 . The expressions
(B.6) and (B.12) are identical and so the steps
from
. The expressions
(B.6) and (B.12) are identical and so the steps
from 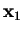 to
to
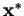 proceed via points which are minima
along each search direction. Taking the scalar product of (B.15)
with
proceed via points which are minima
along each search direction. Taking the scalar product of (B.15)
with 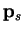 (
(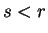 ) instead we obtain
) instead we obtain
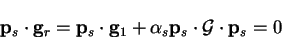 |
(B.16) |
from equation B.12. Thus 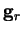 is perpendicular to
all previous search directions so that each point
is perpendicular to
all previous search directions so that each point 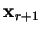 is
actually a minimum with respect to the whole subspace spanned by
is
actually a minimum with respect to the whole subspace spanned by
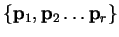 i.e. we can consider each
step as removing one dimension of the space from the problem, so that the
minimum of a quadratic function must always be found in a number of steps
less than or equal to the dimensionality of the space.
i.e. we can consider each
step as removing one dimension of the space from the problem, so that the
minimum of a quadratic function must always be found in a number of steps
less than or equal to the dimensionality of the space.
The method of conjugate gradients uses such a set of conjugate directions
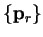 based upon the steepest descent directions
based upon the steepest descent directions
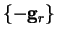 at successive points. For this to be valid, we must show that the gradients
are linearly independent. They are in fact orthogonal, which can be proved by
induction. Starting with
at successive points. For this to be valid, we must show that the gradients
are linearly independent. They are in fact orthogonal, which can be proved by
induction. Starting with
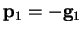 then from the minimum condition (B.4)
we have
then from the minimum condition (B.4)
we have
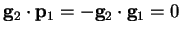 so that the
first two gradients are orthogonal. Then assuming that we have a set of
so that the
first two gradients are orthogonal. Then assuming that we have a set of
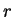 orthogonal gradients, and conjugate directions obtained from them by
(B.9). Using (B.16) we have
orthogonal gradients, and conjugate directions obtained from them by
(B.9). Using (B.16) we have
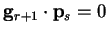 for
for 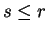 . But
. But 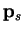 is given by (B.9) as
is given by (B.9) as
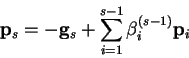 |
(B.17) |
so that
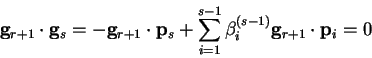 |
(B.18) |
and  is orthogonal to all the previous gradients and the
proof is complete: the gradients are all mutually orthogonal and thus
linearly independent so that they can be used to construct conjugate
directions: the conjugate gradients.
is orthogonal to all the previous gradients and the
proof is complete: the gradients are all mutually orthogonal and thus
linearly independent so that they can be used to construct conjugate
directions: the conjugate gradients.
In this case, equation B.9 becomes
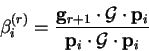 |
(B.19) |
which using (B.7) can be rewritten
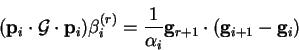 |
(B.20) |
so that by the orthogonality of the gradients,
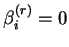 for
for
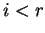 and the only non-vanishing coefficient is
and the only non-vanishing coefficient is 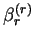 :
:
by (B.16) and (B.9).
Thus the method involves starting by searching along the direction of
steepest descent, finding the minimum point along each direction and then
calculating a new search direction from the new gradient and previous
search direction
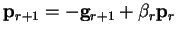 where
where
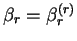 is calculated from either of the
expressions in (B.21, B.22)
(which will differ for a general function) or from
is calculated from either of the
expressions in (B.21, B.22)
(which will differ for a general function) or from
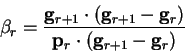 |
(B.23) |
as suggested by Polak [189].
The minimum of the two-dimensional narrow valley, so problematic for the
steepest descents method, is now found in just two steps by the
conjugate gradients method (figure B.2).
Figure B.2:
Conjugate gradients method - only two steps are required to
find the minimum.
|
|




Next: Bibliography
Up: thesis
Previous: A. Bessel function identities
Contents
Peter Haynes
![\includegraphics [height=15cm,angle=-90]{sd.eps}](img1236.gif)
![]() :
:
![]() are said to be conjugate
directions (with respect to
are said to be conjugate
directions (with respect to ![]() ) if they satisfy the condition
) if they satisfy the condition
![]() , not all vanishing,
for which
, not all vanishing,
for which
![]() . But operating on both sides by
. But operating on both sides by
![]() and taking the scalar product with
and taking the scalar product with ![]() implies
implies
![]() for all
for all ![]() by (B.8),
and
by (B.8),
and
![]() since
since ![]() is positive
definite, and so we obtain the contradiction that
is positive
definite, and so we obtain the contradiction that ![]() for all
for all ![]() .
.
![]() using a procedure analogous to
Gram-Schmidt orthogonalisation i.e.
using a procedure analogous to
Gram-Schmidt orthogonalisation i.e. 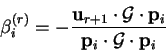
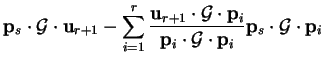
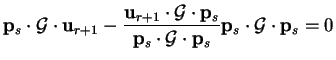
![]() to the minimum
to the minimum
![]() in an
in an ![]() -dimensional space is
-dimensional space is
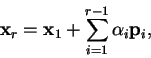
![]() based upon the steepest descent directions
based upon the steepest descent directions
![]() at successive points. For this to be valid, we must show that the gradients
are linearly independent. They are in fact orthogonal, which can be proved by
induction. Starting with
at successive points. For this to be valid, we must show that the gradients
are linearly independent. They are in fact orthogonal, which can be proved by
induction. Starting with
![]() then from the minimum condition (B.4)
we have
then from the minimum condition (B.4)
we have
![]() so that the
first two gradients are orthogonal. Then assuming that we have a set of
so that the
first two gradients are orthogonal. Then assuming that we have a set of
![]() orthogonal gradients, and conjugate directions obtained from them by
(B.9). Using (B.16) we have
orthogonal gradients, and conjugate directions obtained from them by
(B.9). Using (B.16) we have
![]() for
for ![]() . But
. But ![]() is given by (B.9) as
is given by (B.9) as
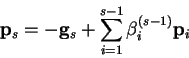
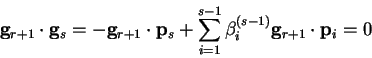
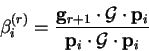
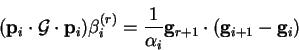
![]() where
where
![]() is calculated from either of the
expressions in (B.21, B.22)
(which will differ for a general function) or from
is calculated from either of the
expressions in (B.21, B.22)
(which will differ for a general function) or from