



Next: 4.5 Requirements for linear-scaling
Up: 4. Density-Matrix Formulation
Previous: 4.3 Density-matrix DFT
Contents
Subsections
4.4 Constraints on the density-matrix
From the definitions so far, the trace of the density-matrix is defined to be
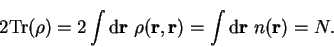 |
(4.26) |
This constraint may be applied explicitly, which is a simple matter given that
this is a linear constraint, or we may prefer to make the Legendre transform
to the zero-temperature grand canonical ensemble and work at fixed chemical
potential and variable electron number, minimising the grand potential
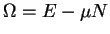 rather than the total energy
rather than the total energy 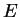 . For insulators, it is
sufficient for the chemical potential
. For insulators, it is
sufficient for the chemical potential 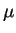 to be between the energies of
the highest occupied and lowest unoccupied states.
to be between the energies of
the highest occupied and lowest unoccupied states.
4.4.2 Idempotency
The self-consistent ground-state density-matrix must display the property of
idempotency i.e. 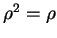 . Unless the eigenvalues of the density-matrix
(occupation numbers) remain in the interval
. Unless the eigenvalues of the density-matrix
(occupation numbers) remain in the interval ![$[0,1]$](img395.gif) the density-matrix
will follow unphysical ``run-away'' solutions. Unfortunately it is not
possible to work directly with the eigenvalues of the density-matrix4.1 to
constrain them to lie in this interval and together with the non-linearity
of the idempotency condition, this constraint turns out to be the major
problem to be tackled. We briefly outline three ways in which this constraint
can be dealt with. The first two of these are related and all three are
described in [134] in the context of Hartree-Fock calculations.
the density-matrix
will follow unphysical ``run-away'' solutions. Unfortunately it is not
possible to work directly with the eigenvalues of the density-matrix4.1 to
constrain them to lie in this interval and together with the non-linearity
of the idempotency condition, this constraint turns out to be the major
problem to be tackled. We briefly outline three ways in which this constraint
can be dealt with. The first two of these are related and all three are
described in [134] in the context of Hartree-Fock calculations.
If we are considering 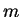 orbitals in our scheme, then the density-matrix in
the representation of those orbitals, or of a linear combination of those
orbitals, is an Hermitian
orbitals in our scheme, then the density-matrix in
the representation of those orbitals, or of a linear combination of those
orbitals, is an Hermitian 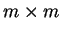 matrix of rank
matrix of rank
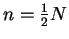 . The factorisation property of idempotent
density-matrices is that an idempotent matrix
. The factorisation property of idempotent
density-matrices is that an idempotent matrix 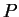 may always be written
may always be written
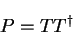 |
(4.27) |
where T is an 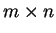 matrix whose columns are orthonormal i.e.
matrix whose columns are orthonormal i.e.
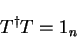 |
(4.28) |
in which 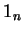 denotes the
denotes the 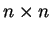 identity matrix.
identity matrix.
Any Hermitian matrix can be diagonalised by some unitary matrix 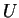 such
that the diagonal matrix
such
that the diagonal matrix 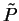 is
is
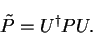 |
(4.29) |
As already observed, the property 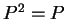 implies
implies
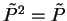 so that each diagonal element (eigenvalue) is zero or one. The rank of
so that each diagonal element (eigenvalue) is zero or one. The rank of 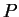 is unchanged by the unitary transformation so that
is unchanged by the unitary transformation so that 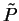 has
has
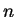 1's and
1's and 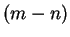 0's on its diagonal. In this case,
0's on its diagonal. In this case,
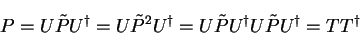 |
(4.30) |
in which 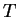 is an
is an 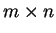 rectangular matrix whose
rectangular matrix whose 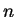 columns are
selected from those of
columns are
selected from those of 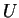 . These columns possess the required orthonormality
from the unitary property of
. These columns possess the required orthonormality
from the unitary property of 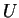 and the proof of the factorisation property
is complete.
and the proof of the factorisation property
is complete.
We also note that expressing the density-matrix in this way guarantees that
it is positive semi-definite
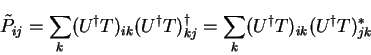 |
(4.31) |
so that the eigenvalues are (no summation convention)
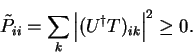 |
(4.32) |
4.4.3 Penalty functional
Consider a matrix 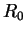 which is not idempotent i.e.
which is not idempotent i.e.
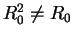 .
To make it so, we need to reduce the matrix
.
To make it so, we need to reduce the matrix 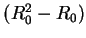 to zero, which
can be achieved by minimising the (positive semi-definite) scalar quantity
to zero, which
can be achieved by minimising the (positive semi-definite) scalar quantity
![${\rm Tr}\left[(R_0^2 - R_0)^2\right]$](img455.gif) , whose minimum value is zero, with respect to the
individual elements. Since
, whose minimum value is zero, with respect to the
individual elements. Since
![\begin{displaymath}
\frac{\partial {\rm Tr}\left[(R_0^2 - R_0)^2\right]}{\partial (R_0)_{ij}} =
\left[ 2R_0(R_0-1)(2R_0-1)\right]_{ji} ,
\end{displaymath}](img456.gif) |
(4.33) |
this can be achieved by using the right-hand side of this equation as a
search direction in a steepest descents or conjugate gradients scheme.
This results in a rapidly convergent (second order) sequence 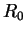 ,
, 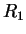 ,
,
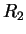 etc. which in the steepest descents method is defined by
etc. which in the steepest descents method is defined by
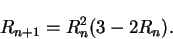 |
(4.34) |
The limit 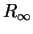 is a strictly idempotent matrix close to
is a strictly idempotent matrix close to 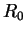 in the sense that the separation
in the sense that the separation
![\begin{displaymath}
{\rm Tr}\left[(R_{\infty}-R_0)^2\right] \ll {\rm Tr}(R_{\infty}) = n .
\end{displaymath}](img461.gif) |
(4.35) |
Kohn [135] has suggested the use of the square-root of this
function as a penalty functional for the density-matrix:
![\begin{displaymath}
{\cal P}[\rho] = \left[ \int {\mathrm d}{\bf r} \left( \rho^2 (1-\rho)^2
\right)({\bf r},{\bf r}) \right]^{1 \over 2}
\end{displaymath}](img462.gif) |
(4.36) |
and has proved that the minimum of the functional
equals the ground-state grand potential (i.e.
![${\cal P}[\rho] = 0$](img464.gif) ) for some
) for some
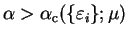 . In particular,
. In particular,
![\begin{displaymath}
\alpha_{\mathrm c} > 2 \left[ \sum_{i,\varepsilon_i \leq \mu}
(\varepsilon_i - \mu)^2 \right]^{1 \over 2}
\end{displaymath}](img466.gif) |
(4.37) |
although he does not prove that this is a lower bound. A practical scheme
would increase the value of  until the minimum of the functional
occurred for
until the minimum of the functional
occurred for
![${\cal P}[\rho] = 0$](img464.gif) , and this is discussed more fully in section
6.1.
, and this is discussed more fully in section
6.1.
4.4.4 Purifying transformation
We consider the result of one steepest descent step i.e. one iteration of
equation 4.34 which allows us to write the density-matrix 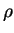 in terms of an auxiliary matrix
in terms of an auxiliary matrix 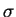 as
as
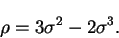 |
(4.38) |
The second order convergence is exhibited by
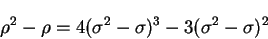 |
(4.39) |
so that if 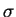 is a nearly idempotent matrix (in a manner to be defined
below), then
is a nearly idempotent matrix (in a manner to be defined
below), then 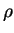 constructed from
constructed from 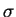 by (4.38) is a
more nearly idempotent matrix, with leading error second-order in the error
of
by (4.38) is a
more nearly idempotent matrix, with leading error second-order in the error
of 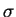 .
.
In the common diagonal representation of 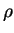 and
and 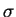 this relationship
can be expressed in terms of the individual eigenvalues
this relationship
can be expressed in terms of the individual eigenvalues
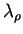 and
and
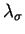 :
:
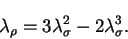 |
(4.40) |
Figure 4.1:
Behaviour of eigenvalues under the purifying transformation.
|
|
Thus as long as all of the eigenvalues of 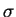 lie in the interval
lie in the interval
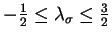 the eigenvalues of
the eigenvalues of
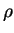 will lie in the interval
will lie in the interval
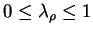 as required.
If any of the eigenvalues of
as required.
If any of the eigenvalues of 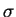 lie outside the interval
lie outside the interval
![$[ {1 - \surd{5} \over 2},{1 + \surd{5} \over 2}]$](img476.gif) , then
, then 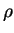 as constructed by (4.38) will be less idempotent than
as constructed by (4.38) will be less idempotent than
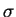 , and this defines the meaning of ``nearly idempotent'' for
, and this defines the meaning of ``nearly idempotent'' for 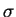 .
Run-away solutions are still possible when the purifying
transformation is used to construct
.
Run-away solutions are still possible when the purifying
transformation is used to construct 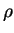 , but at least there is now a
metastable minimum at the ground-state, and variation of
, but at least there is now a
metastable minimum at the ground-state, and variation of
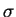 will implicitly drive
will implicitly drive 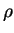 to idempotency.
to idempotency.
4.4.5 Idempotency-preserving variations
Finally we consider the most general change which an idempotent 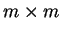 matrix of rank
matrix of rank 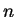 can suffer, while maintaining that idempotency. Using
the factorisation property we write
can suffer, while maintaining that idempotency. Using
the factorisation property we write
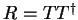 and consider changes
in
and consider changes
in 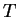 i.e.
i.e.
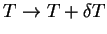 , where, without loss of generality,
, where, without loss of generality,
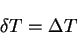 |
(4.41) |
in which 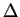 is an arbitrary non-singular
is an arbitrary non-singular 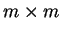 matrix. Now the
density-matrix
matrix. Now the
density-matrix 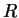 is a projection operator associated with an
is a projection operator associated with an
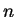 -dimensional vector subspace (
-dimensional vector subspace (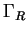 ) spanned by the columns of
) spanned by the columns of 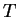 .
Any vector
.
Any vector 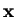 may of course be uniquely decomposed into its
components lying in the subspace
may of course be uniquely decomposed into its
components lying in the subspace 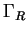 and in the complementary
subspace
and in the complementary
subspace 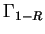 :
:
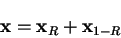 |
(4.42) |
where
To define a new matrix 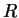 it is sufficient to define a new
it is sufficient to define a new 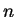 -dimensional
subspace. Since any vector can be decomposed according to equation
4.42, including the columns of
-dimensional
subspace. Since any vector can be decomposed according to equation
4.42, including the columns of 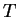 , any new vector (of
arbitrary length) can be formed by adding a vector lying
completely outside
, any new vector (of
arbitrary length) can be formed by adding a vector lying
completely outside 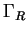 .
.
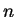 arbitrary linearly-independent vectors of this kind are given by the
columns of
arbitrary linearly-independent vectors of this kind are given by the
columns of
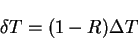 |
(4.45) |
in which the action of 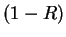 is to project out the part of
is to project out the part of  lying in
lying in 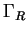 . So
. So 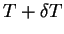 with
with 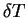 defined by
(4.45) defines a new subspace in a completely general way.
However the columns of
defined by
(4.45) defines a new subspace in a completely general way.
However the columns of
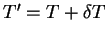 are no longer orthonormal and so
it is necessary to orthonormalise the columns of
are no longer orthonormal and so
it is necessary to orthonormalise the columns of 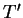 to obtain a new set
to obtain a new set
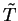 which defines the new projection operator
which defines the new projection operator
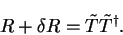 |
(4.46) |
The metric associated with the vectors of 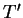 is the
is the 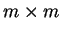 matrix
matrix
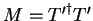 and so a convenient orthonormalisation is
and so a convenient orthonormalisation is
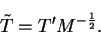 |
(4.47) |
Defining
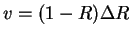 we note the following relations, following from
we note the following relations, following from
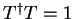 and
and
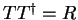 .
.
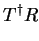 |
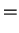 |
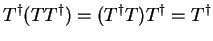 |
(4.48) |
 |
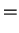 |
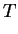 |
(4.49) |
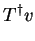 |
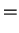 |
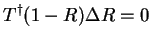 |
(4.50) |
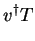 |
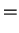 |
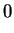 |
(4.51) |
Thus 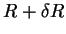
When 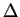 represents a small change, then a convergent expansion for the
inverse matrix in equation 4.52 can be used
represents a small change, then a convergent expansion for the
inverse matrix in equation 4.52 can be used
![\begin{displaymath}
\left[ 1 + v^{\dag } v \right]^{-1} = \sum_{n=0}^{\infty} (-1)^n (v^{\dag } v)^n
\end{displaymath}](img517.gif) |
(4.53) |
to write down 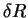 to any order
to any order
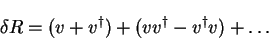 |
(4.54) |
By taking the expansion to first order only, we make the change 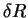 linear in
linear in 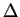 (which has certain advantages e.g. in implementing conjugate gradients) and see that this
does indeed maintain idempotency to first order:
(which has certain advantages e.g. in implementing conjugate gradients) and see that this
does indeed maintain idempotency to first order:
which vanishes to first order in 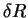 as required. Thus if we have the
ground-state density-matrix and consider making variations consistent with
idempotency to first order as described here, then the energy must
increase, and again some stability against the run-away solutions is
obtained.
as required. Thus if we have the
ground-state density-matrix and consider making variations consistent with
idempotency to first order as described here, then the energy must
increase, and again some stability against the run-away solutions is
obtained.




Next: 4.5 Requirements for linear-scaling
Up: 4. Density-Matrix Formulation
Previous: 4.3 Density-matrix DFT
Contents
Peter Haynes
![]() . Unless the eigenvalues of the density-matrix
(occupation numbers) remain in the interval
. Unless the eigenvalues of the density-matrix
(occupation numbers) remain in the interval ![]() the density-matrix
will follow unphysical ``run-away'' solutions. Unfortunately it is not
possible to work directly with the eigenvalues of the density-matrix4.1 to
constrain them to lie in this interval and together with the non-linearity
of the idempotency condition, this constraint turns out to be the major
problem to be tackled. We briefly outline three ways in which this constraint
can be dealt with. The first two of these are related and all three are
described in [134] in the context of Hartree-Fock calculations.
the density-matrix
will follow unphysical ``run-away'' solutions. Unfortunately it is not
possible to work directly with the eigenvalues of the density-matrix4.1 to
constrain them to lie in this interval and together with the non-linearity
of the idempotency condition, this constraint turns out to be the major
problem to be tackled. We briefly outline three ways in which this constraint
can be dealt with. The first two of these are related and all three are
described in [134] in the context of Hartree-Fock calculations.
![]() orbitals in our scheme, then the density-matrix in
the representation of those orbitals, or of a linear combination of those
orbitals, is an Hermitian
orbitals in our scheme, then the density-matrix in
the representation of those orbitals, or of a linear combination of those
orbitals, is an Hermitian ![]() matrix of rank
matrix of rank
![]() . The factorisation property of idempotent
density-matrices is that an idempotent matrix
. The factorisation property of idempotent
density-matrices is that an idempotent matrix ![]() may always be written
may always be written
![]() such
that the diagonal matrix
such
that the diagonal matrix ![]() is
is
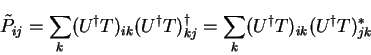
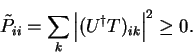
![]() which is not idempotent i.e.
which is not idempotent i.e.
![]() .
To make it so, we need to reduce the matrix
.
To make it so, we need to reduce the matrix ![]() to zero, which
can be achieved by minimising the (positive semi-definite) scalar quantity
to zero, which
can be achieved by minimising the (positive semi-definite) scalar quantity
![]() , whose minimum value is zero, with respect to the
individual elements. Since
, whose minimum value is zero, with respect to the
individual elements. Since
![\begin{displaymath}
\frac{\partial {\rm Tr}\left[(R_0^2 - R_0)^2\right]}{\partial (R_0)_{ij}} =
\left[ 2R_0(R_0-1)(2R_0-1)\right]_{ji} ,
\end{displaymath}](img456.gif)
![\begin{displaymath}
\alpha_{\mathrm c} > 2 \left[ \sum_{i,\varepsilon_i \leq \mu}
(\varepsilon_i - \mu)^2 \right]^{1 \over 2}
\end{displaymath}](img466.gif)
![]() in terms of an auxiliary matrix
in terms of an auxiliary matrix ![]() as
as
![]() and
and ![]() this relationship
can be expressed in terms of the individual eigenvalues
this relationship
can be expressed in terms of the individual eigenvalues
![]() and
and
![]() :
:
![]() matrix of rank
matrix of rank ![]() can suffer, while maintaining that idempotency. Using
the factorisation property we write
can suffer, while maintaining that idempotency. Using
the factorisation property we write
![]() and consider changes
in
and consider changes
in ![]() i.e.
i.e.
![]() , where, without loss of generality,
, where, without loss of generality,
![]() it is sufficient to define a new
it is sufficient to define a new ![]() -dimensional
subspace. Since any vector can be decomposed according to equation
4.42, including the columns of
-dimensional
subspace. Since any vector can be decomposed according to equation
4.42, including the columns of ![]() , any new vector (of
arbitrary length) can be formed by adding a vector lying
completely outside
, any new vector (of
arbitrary length) can be formed by adding a vector lying
completely outside ![]() .
.
![]() arbitrary linearly-independent vectors of this kind are given by the
columns of
arbitrary linearly-independent vectors of this kind are given by the
columns of
![]() is the
is the ![]() matrix
matrix
![]() and so a convenient orthonormalisation is
and so a convenient orthonormalisation is
![\begin{displaymath}
\left[ 1 + v^{\dag } v \right]^{-1} = \sum_{n=0}^{\infty} (-1)^n (v^{\dag } v)^n
\end{displaymath}](img517.gif)
![]() linear in
linear in ![]() (which has certain advantages e.g. in implementing conjugate gradients) and see that this
does indeed maintain idempotency to first order:
(which has certain advantages e.g. in implementing conjugate gradients) and see that this
does indeed maintain idempotency to first order: