



Next: 4.3 Density-matrix DFT
Up: 4. Density-Matrix Formulation
Previous: 4.1 The density-matrix
Contents
4.2 Partial occupation of the Kohn-Sham orbitals
In the Kohn-Sham scheme, the single-particle orbitals
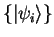 were either empty or doubly occupied (two spin states). It will prove to be
useful if we now
generalise to include partial occupation [131] so that
each orbital contains
were either empty or doubly occupied (two spin states). It will prove to be
useful if we now
generalise to include partial occupation [131] so that
each orbital contains 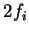 electrons where
electrons where
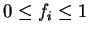 . The
electronic density is now defined as
. The
electronic density is now defined as
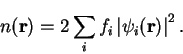 |
(4.6) |
Following the constrained search formulation we now define a generalised
non-interacting kinetic energy functional
![$T_{\mathrm s}^{\mathrm J}[n]$](img399.gif) as
as
![\begin{displaymath}
T_{\mathrm s}^{\mathrm J}[n] = \mathop{\rm min}\limits _{\{f...
...ft( - {\textstyle{1 \over 2}} \nabla^2 \right) \psi_i({\bf r})
\end{displaymath}](img400.gif) |
(4.7) |
where the search is over all orthonormal orbitals
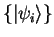 and
occupation numbers
and
occupation numbers 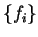 which yield the density
which yield the density 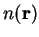 (which
implies that
(which
implies that
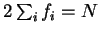 ).
).
Janak's functional is defined as
![\begin{displaymath}
E_V^{\mathrm J}[\{f_i\},\{\vert\psi_i\rangle\}] = 2 \sum_i f...
...\int {\mathrm d}{\bf r}~n({\bf r}) V_{\mathrm{ext}}({\bf r}) .
\end{displaymath}](img403.gif) |
(4.8) |
The minimisation is now performed with respect to both the occupation
numbers 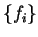 and the orbitals
and the orbitals
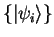 .
.
For a fixed set of occupation numbers, the Euler-Lagrange equations for the
variation of the functional with respect to the orbitals again yield
Schrödinger-like equations:
![\begin{displaymath}
\left[ -\textstyle{1 \over 2} f_i \nabla^2 + f_i V_{\mathrm{...
...
({\bf r}) \right]
\psi_i({\bf r}) = \lambda_i \psi_i({\bf r})
\end{displaymath}](img404.gif) |
(4.9) |
in which we can identify
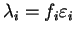 to obtain the
Kohn-Sham equations
to obtain the
Kohn-Sham equations
![\begin{displaymath}
\left[ -\textstyle{1 \over 2} \nabla^2 + V_{\mathrm{KS}}
({\bf r}) \right]
\psi_i({\bf r}) = \varepsilon_i \psi_i({\bf r}) .
\end{displaymath}](img406.gif) |
(4.10) |
Multiplying by
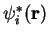 and integrating gives
and integrating gives
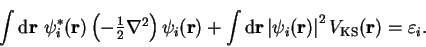 |
(4.11) |
We obtain the dependence of the energy functional on the occupation numbers
by varying one of the 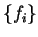 while allowing the orbitals to relax (i.e. solving equations 4.6 and 4.10 self-consistently).
We define the kinetic energy for orbital
while allowing the orbitals to relax (i.e. solving equations 4.6 and 4.10 self-consistently).
We define the kinetic energy for orbital 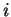 ,
, 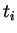 , by
, by
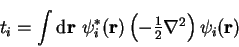 |
(4.12) |
in terms of which the generalised kinetic energy functional
![$T_{\mathrm s}^{\mathrm J}[n]$](img399.gif) is
is
![\begin{displaymath}
T_{\mathrm s}^{\mathrm J}[n] = 2 \sum_i f_i~t_i .
\end{displaymath}](img411.gif) |
(4.13) |
Then
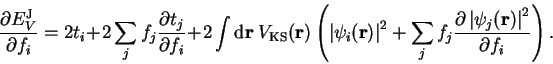 |
(4.14) |
Using equation 4.11 we can rewrite the terms not involving a summation
over orbitals:
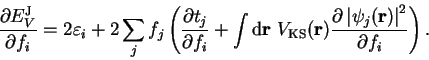 |
(4.15) |
From the definition of 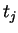 (4.12) we obtain
(4.12) we obtain
![\begin{displaymath}
\frac{\partial t_j}{\partial f_i} = \int {\mathrm d}{\bf r}
...
...right)
\frac{\partial \psi_j({\bf r})}{\partial f_i} \right] .
\end{displaymath}](img415.gif) |
(4.16) |
Substituting this result in equation 4.15 we obtain for the
second term on the right-hand side
![\begin{displaymath}
2 \sum_j f_j \int {\mathrm d}{\bf r} \left[ \frac{\partial \...
...right)
\frac{\partial \psi_j({\bf r})}{\partial f_i} \right] .
\end{displaymath}](img416.gif) |
(4.17) |
Now using equation 4.10 we find
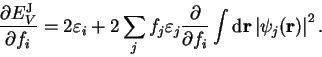 |
(4.18) |
The second term on the right-hand side vanishes since the orbitals are
normalised and so the final result is that
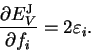 |
(4.19) |
Variation of the functional subject to the constraint of constant electron
number (i.e. unconstrained variation of
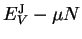 ) gives
) gives
![\begin{displaymath}
\delta [ E_V^{\mathrm J} - \mu N ] = 2 \sum_i (\varepsilon_i - \mu) \delta f_i .
\end{displaymath}](img420.gif) |
(4.20) |
This generalised functional is not variational with respect to arbitrary variations in
the occupation numbers [132]. Objections have been raised
[133] to considering occupation numbers other than zero or one
in zero-temperature density-functional theory, but the conclusion is still
that at self-consistency, orbitals above the Fermi energy are unoccupied and
orbitals below are fully occupied, and we recall that this state of affairs
corresponds to an idempotent density-matrix.
If the occupation numbers are allowed to vary in the interval ![$[0,1]$](img395.gif) we see
that the lowest value of the generalised functional is obtained for the
correct choice of occupation numbers outlined above. However, if the occupation
numbers are allowed to vary outside this interval, this result no longer
holds since the energy can be lowered by over-filling (
we see
that the lowest value of the generalised functional is obtained for the
correct choice of occupation numbers outlined above. However, if the occupation
numbers are allowed to vary outside this interval, this result no longer
holds since the energy can be lowered by over-filling (
 ) orbitals below the Fermi level, or negatively filling (
) orbitals below the Fermi level, or negatively filling (
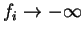 ) orbitals above the Fermi level, while still keeping the sum of the
occupation numbers
correct. Constraining the occupation numbers to avoid these unphysical
situations is discussed in section 4.4.
) orbitals above the Fermi level, while still keeping the sum of the
occupation numbers
correct. Constraining the occupation numbers to avoid these unphysical
situations is discussed in section 4.4.




Next: 4.3 Density-matrix DFT
Up: 4. Density-Matrix Formulation
Previous: 4.1 The density-matrix
Contents
Peter Haynes
![]() were either empty or doubly occupied (two spin states). It will prove to be
useful if we now
generalise to include partial occupation [131] so that
each orbital contains
were either empty or doubly occupied (two spin states). It will prove to be
useful if we now
generalise to include partial occupation [131] so that
each orbital contains ![]() electrons where
electrons where
![]() . The
electronic density is now defined as
. The
electronic density is now defined as
![\begin{displaymath}
T_{\mathrm s}^{\mathrm J}[n] = \mathop{\rm min}\limits _{\{f...
...ft( - {\textstyle{1 \over 2}} \nabla^2 \right) \psi_i({\bf r})
\end{displaymath}](img400.gif)
![\begin{displaymath}
E_V^{\mathrm J}[\{f_i\},\{\vert\psi_i\rangle\}] = 2 \sum_i f...
...\int {\mathrm d}{\bf r}~n({\bf r}) V_{\mathrm{ext}}({\bf r}) .
\end{displaymath}](img403.gif)
![]() while allowing the orbitals to relax (i.e. solving equations 4.6 and 4.10 self-consistently).
We define the kinetic energy for orbital
while allowing the orbitals to relax (i.e. solving equations 4.6 and 4.10 self-consistently).
We define the kinetic energy for orbital ![]() ,
, ![]() , by
, by
![\begin{displaymath}
T_{\mathrm s}^{\mathrm J}[n] = 2 \sum_i f_i~t_i .
\end{displaymath}](img411.gif)
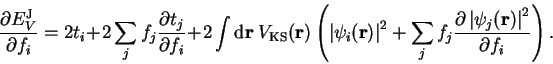
![\begin{displaymath}
\frac{\partial t_j}{\partial f_i} = \int {\mathrm d}{\bf r}
...
...right)
\frac{\partial \psi_j({\bf r})}{\partial f_i} \right] .
\end{displaymath}](img415.gif)
![\begin{displaymath}
2 \sum_j f_j \int {\mathrm d}{\bf r} \left[ \frac{\partial \...
...right)
\frac{\partial \psi_j({\bf r})}{\partial f_i} \right] .
\end{displaymath}](img416.gif)
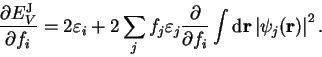
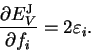
![]() ) gives
) gives
![]() we see
that the lowest value of the generalised functional is obtained for the
correct choice of occupation numbers outlined above. However, if the occupation
numbers are allowed to vary outside this interval, this result no longer
holds since the energy can be lowered by over-filling (
we see
that the lowest value of the generalised functional is obtained for the
correct choice of occupation numbers outlined above. However, if the occupation
numbers are allowed to vary outside this interval, this result no longer
holds since the energy can be lowered by over-filling (
![]() ) orbitals below the Fermi level, or negatively filling (
) orbitals below the Fermi level, or negatively filling (
![]() ) orbitals above the Fermi level, while still keeping the sum of the
occupation numbers
correct. Constraining the occupation numbers to avoid these unphysical
situations is discussed in section 4.4.
) orbitals above the Fermi level, while still keeping the sum of the
occupation numbers
correct. Constraining the occupation numbers to avoid these unphysical
situations is discussed in section 4.4.