Hartree, local pseudopotential, and exchange-correlation energy

The matrix elements of the Hartree, the local pseudopotential and the exchange-correlation potential may be treated together:

$$V_{\mathrm{Hlxc,\alpha\beta}} = \langle \phi_{\alpha} \vert \left[ V_{\mathrm{H}}(\mathbf{r}) + V... ...mathbf{r}) \right]_{B} + V_{\mathrm{xc}}(\mathbf{r}) \vert \phi_{\beta} \rangle$$

$$\simeq \langle \phi_{\alpha} \vert \left( \left[ V_{\mathrm{H}}(\mathbf{... ...r}) + V_{\mathrm{xc}}(\mathbf{r}) \right]_{B} \phi_{\beta} \right)_{D} \rangle,$$ (34)

where the approximation is due to the inability to faithfully represent the exchange-correlation energy-density on the fine grid. The operator defined by

$$\left[ V_{\mathrm{Hlxc}}(\mathbf{r}) \right]_{B} \equiv \lef... ...rm{loc}}(\mathbf{r}) + V_{\mathrm{xc}}(\mathbf{r}) \right]_{B}$$ (35)

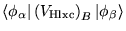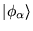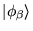extends over the fine grid of the whole simulation cell. We calculate matrix elements $\langle\phi_{\alpha}\vert \left( V_{\mathrm{Hlxc}} \right)_{B} \vert\phi_{\beta}\rangle$, for a pair of overlapping NGWFs, $\vert\phi_{\alpha}\rangle$ and $\vert\phi_{\beta}\rangle$, by projecting 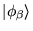$\vert\phi_{\beta}\rangle$ onto the FFT box that encloses the pair of functions. This NGWF is then interpolated onto the fine grid of the FFT box. 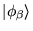$\left[ V_{\mathrm{Hlxc}}(\mathbf{r}) \right]_{B}$ is projected onto the fine grid of the FFT box and its product taken with $\vert\phi_{\beta}\rangle$ on the grid points. The result is Fourier filtered onto the standard grid of the FFT box, thus keeping only frequency components represented through the standard grid basis functions, 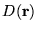$D(\mathbf{r})$, and projected back onto the standard grid of the simulation cell. The matrix element is then obtained by computing the overlap with 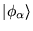$\vert\phi_{\alpha}\rangle$ by summation over the grid points enclosed within its localisation region. This procedure may be represented as

$$V^{\mathrm{box}}_{\mathrm{Hlxc,\alpha\beta}} = \langle\phi_{\alpha}\vert \left( V^{\mathrm{box}}_{\mathrm{Hlxc}} \right)_{B} \vert\phi_{\beta}\rangle$$

$$= \langle\phi_{\alpha}\vert\hat{P}^{\dagger}(\alpha\beta) \left[ \h... ...athrm{Hlxc}} \right)_{B} \right] \hat{P}(\alpha\beta)\vert\phi_{\beta}\rangle ,$$ (36)

and since all computations are done using the FFT box, the matrix elements can be calculated in 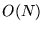$O(N)$ operations.

Finally, the total energy, calculated using our FFT box method, may be written as

$$E^{\mathrm{box}}[n] = 2K^{\alpha\beta}H_{\beta\alpha}^{\mathrm{box}} - E^{\mathrm{box}}_{\mathrm{DC}}[n],$$ (37)

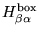where $H_{\beta\alpha}^{\mathrm{box}}$ is given by

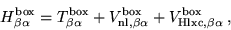$$H_{\beta\alpha}^{\mathrm{box}} = T_{\beta\alpha}^{\mathrm{bo... ...thrm{box}} + V_{\mathrm{Hlxc},\beta\alpha}^{\mathrm{box}} ,$$ (38)

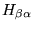and $E^{\mathrm{box}}_{\mathrm{DC}}[n]$ is as defined in equation (18), but with the charge density calculated according to equation (33). The FFT box method enables the sparse matrix represented by $H_{\beta\alpha}$ to be computed with an effort that scales linearly with system size. With just one extra variational approximation, namely truncation of the density kernel, the charge density of equation (33) and hence total energy of equation (37) may be calculated in 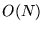$O(N)$ operations.