

Next: Total energy using the
Up: Total-energy calculations on a
Previous: Basis set
Total energy
In terms of the set of NGWFs
 , the single-particle density matrix in the co-ordinate representation is expressed as
, the single-particle density matrix in the co-ordinate representation is expressed as
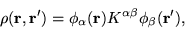 |
(5) |
where the density kernel,
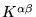 , is the matrix representation of the density matrix in terms of the contravariant duals of the NGWFs [15,16]. The NGWFs are real, as we are concerned only with calculations at the
, is the matrix representation of the density matrix in terms of the contravariant duals of the NGWFs [15,16]. The NGWFs are real, as we are concerned only with calculations at the 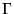 -point. Summation over repeated Greek indices is assumed throughout.
-point. Summation over repeated Greek indices is assumed throughout.
The charge density is given by,
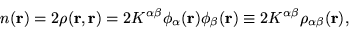 |
(6) |
where
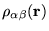 is defined as,
is defined as,
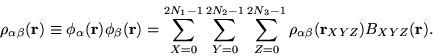 |
(7) |
This quantity is expanded in terms of the basis functions of the fine grid,
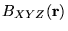 (see Appendix A) because the density needs to be represented in terms of a basis with twice the cut-off frequency of the NGWFs.
(see Appendix A) because the density needs to be represented in terms of a basis with twice the cut-off frequency of the NGWFs.
Neglecting the contribution due to the fixed background of ionic charges, the total energy, ![$E[n]$](img44.png) , of the system is the sum of the kinetic energy (
, of the system is the sum of the kinetic energy (
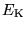 ), the Hartree energy (
), the Hartree energy (
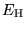 ), the local pseudopotential energy (
), the local pseudopotential energy (
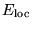 ), the non-local pseudopotential energy (
), the non-local pseudopotential energy (
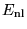 ), and the exchange-correlation energy (
), and the exchange-correlation energy (
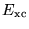 ).
).
The kinetic energy is given by
where 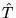 is related to the Laplacian operator by
is related to the Laplacian operator by
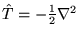 . This is most conveniently applied in reciprocal space, where it is diagonal. We see that the kinetic energy involves matrix elements of the form
. This is most conveniently applied in reciprocal space, where it is diagonal. We see that the kinetic energy involves matrix elements of the form
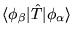 . Thus, one way of proceeding would be to FFT
. Thus, one way of proceeding would be to FFT 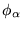 in the whole simulation cell, apply the Laplacian, FFT back and perform the integral over real space as a summation over grid points as suggested by equation (52). If
in the whole simulation cell, apply the Laplacian, FFT back and perform the integral over real space as a summation over grid points as suggested by equation (52). If 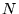 is the number of grid points in the simulation cell (which is proportional to system size), this procedure has a computational cost that scales as
is the number of grid points in the simulation cell (which is proportional to system size), this procedure has a computational cost that scales as 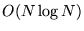 for each NGWF and hence as
for each NGWF and hence as
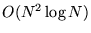 overall. We will see later how linear-scaling can be achieved for all the terms that compose
overall. We will see later how linear-scaling can be achieved for all the terms that compose ![$E[n]$](img44.png) .
.
The Hartree energy is given by,
where the Hartree potential
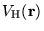 is,
is,
We see that
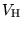 is the result of a convolution between the charge density and the Coulomb potential, and is thus represented by the fine grid basis functions.
is the result of a convolution between the charge density and the Coulomb potential, and is thus represented by the fine grid basis functions.
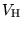 is calculated on the fine grid in reciprocal space, where the real space convolution becomes a simple product, and fast Fourier transformed back to real space.
is calculated on the fine grid in reciprocal space, where the real space convolution becomes a simple product, and fast Fourier transformed back to real space. 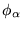 is Fourier interpolated onto the fine grid and its product with
is Fourier interpolated onto the fine grid and its product with
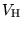 taken. The result is Fourier filtered to the standard grid, and the matrix elements
taken. The result is Fourier filtered to the standard grid, and the matrix elements
![$\langle\phi_{\beta}\vert\left[ V_{\mathrm{H}}\phi_{\alpha} \right]_{D} \rangle$](img67.png) calculated by summation over the grid points of the standard grid, where the subscript
calculated by summation over the grid points of the standard grid, where the subscript 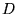 shows that we only need to consider frequency components represented by the basis functions
shows that we only need to consider frequency components represented by the basis functions
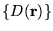 as shown in equation (52).
as shown in equation (52).
The local pseudopotential energy is given by the integral
![\begin{displaymath}
E_{\mathrm{loc}}[n] = \int d\mathbf{r} \: V_{\mathrm{loc}}(\...
...\left[ V_{\mathrm{loc}}(\mathbf{r}) \right]_{B} n(\mathbf{r}),
\end{displaymath}](img70.png) |
(11) |
where the second equality makes use of equation (56), and the subscript 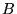 shows that only frequency components represented by the fine grid basis functions,
shows that only frequency components represented by the fine grid basis functions,
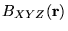 , need to be considered. Thus, it may be calculated in the same way as the Hartree energy:
, need to be considered. Thus, it may be calculated in the same way as the Hartree energy:
The non-local pseudopotential energy is given by
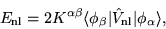 |
(13) |
where the non-local pseudopotential operator
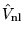 that we use is in Kleinman-Bylander form [17],
that we use is in Kleinman-Bylander form [17],
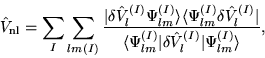 |
(14) |
where the first summation is over the atoms 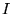 , and the second is over the angular momentum components for each atom.
, and the second is over the angular momentum components for each atom.
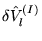 is the angular momentum dependent part of the atomic pseudopotential and the
is the angular momentum dependent part of the atomic pseudopotential and the
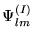 are its associated pseudo-orbitals. We see that the matrix elements of the non-local potential involve the calculation of integrals of the form
are its associated pseudo-orbitals. We see that the matrix elements of the non-local potential involve the calculation of integrals of the form
![$\langle\phi_{\beta}\vert\delta \hat{V}_{l}^{(I)}\Psi_{lm}^{(I)}\rangle = \langl...
..._{\beta}\vert \left[ \delta \hat{V}_{l}^{(I)}\Psi_{lm}^{(I)} \right]_{D}\rangle$](img81.png) , which may be performed by summation over the standard real space grid.
, which may be performed by summation over the standard real space grid.
The exchange-correlation energy within the LDA is given by approximating the integral over the exchange-correlation energy density,
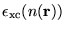 , by a summation over the points of the fine grid:
, by a summation over the points of the fine grid:
This is approximate as the fine grid cannot represent the exchange-correlation energy density without some aliasing. The errors associated with this approximation are expected to be similar to those encountered in traditional plane-wave codes [1].
We may write the total energy as,
![\begin{displaymath}
E[n] = 2K^{\alpha\beta}H_{\beta\alpha} - E_{\mathrm{DC}}[n],
\end{displaymath}](img87.png) |
(16) |
where the matrix elements of the Kohn-Sham Hamiltonian are given by,
![\begin{displaymath}
H_{\beta\alpha} = \langle\phi_{\beta}\vert\left[ \hat{T} + V...
... V_{\mathrm{xc}}(\mathbf{r})\right] \vert\phi_{\alpha}\rangle,
\end{displaymath}](img88.png) |
(17) |
![$V_{xc}(\mathbf{r}) = \frac{\delta E_{\mathrm{xc}}[n]}{\delta n(\mathbf{r})}$](img89.png) is the exchange-correlation potential, and
is the exchange-correlation potential, and
![$E_{\mathrm{DC}}[n]$](img90.png) is the double-counting correction,
is the double-counting correction,
![\begin{displaymath}
E_{\mathrm{DC}}[n] = \frac{1}{2}\int d\mathbf{r} \: n(\mathb...
...(\mathbf{r}) V_{\mathrm{xc}}(\mathbf{r}) - E_{\mathrm{xc}}[n].
\end{displaymath}](img91.png) |
(18) |
As we are dealing with a sparse system, the number of non-zero matrix elements will be proportional to the system size in the limit of large systems. The procedure outlined above for calculating each of these matrix elements has a computational cost that scales as 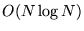 for each element. This is because FFTs of NGWFs are performed over the entire simulation cell. Thus the cost of computing all non-zero matrix elements scales as
for each element. This is because FFTs of NGWFs are performed over the entire simulation cell. Thus the cost of computing all non-zero matrix elements scales as
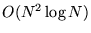 .
.


Next: Total energy using the
Up: Total-energy calculations on a
Previous: Basis set
Peter D. Haynes
2002-10-29
![]() , of the system is the sum of the kinetic energy (
, of the system is the sum of the kinetic energy (
![]() ), the Hartree energy (
), the Hartree energy (
![]() ), the local pseudopotential energy (
), the local pseudopotential energy (
![]() ), the non-local pseudopotential energy (
), the non-local pseudopotential energy (
![]() ), and the exchange-correlation energy (
), and the exchange-correlation energy (
![]() ).
).
![]() is calculated on the fine grid in reciprocal space, where the real space convolution becomes a simple product, and fast Fourier transformed back to real space.
is calculated on the fine grid in reciprocal space, where the real space convolution becomes a simple product, and fast Fourier transformed back to real space. ![]() is Fourier interpolated onto the fine grid and its product with
is Fourier interpolated onto the fine grid and its product with
![]() taken. The result is Fourier filtered to the standard grid, and the matrix elements
taken. The result is Fourier filtered to the standard grid, and the matrix elements
![]() calculated by summation over the grid points of the standard grid, where the subscript
calculated by summation over the grid points of the standard grid, where the subscript ![]() shows that we only need to consider frequency components represented by the basis functions
shows that we only need to consider frequency components represented by the basis functions
![]() as shown in equation (52).
as shown in equation (52).
![]() , by a summation over the points of the fine grid:
, by a summation over the points of the fine grid:
![]() for each element. This is because FFTs of NGWFs are performed over the entire simulation cell. Thus the cost of computing all non-zero matrix elements scales as
for each element. This is because FFTs of NGWFs are performed over the entire simulation cell. Thus the cost of computing all non-zero matrix elements scales as
![]() .
.