Charge density

The charge density of equation (6) is a quantity that extends over the entire simulation cell. The individual contributions to the charge density, i.e., the 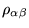$\rho_{\alpha\beta}$ of equation (7), however, are localised in real space and may thus be calculated using the FFT box with a cost that is independent of system-size. 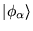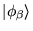For a given pair of overlapping NGWFs, $\vert\phi_{\alpha}\rangle$ and $\vert\phi_{\beta}\rangle$, we project them from the simulation cell into their FFT box. Both are then interpolated onto the fine grid of the FFT box using fast Fourier transforms and zero-padding in reciprocal space. The cost associated with this procedure is system-size independent as it is done over the grid points of the FFT box only. The interpolated NGWFs are multiplied together on the fine grid points of the FFT box and the result projected back onto the fine grid of the simulation cell. In terms of our projection operators, this becomes

$$\rho_{\alpha\beta}^{\mathrm{box}}(\mathbf{r}) = \hat{Q}^{\da... ...hat{P}(\alpha\beta)\phi_{\beta}(\mathbf{r}) \right) \right] .$$ (32)

The total charge density is then built up by summing all the contributions from the FFT boxes of pairs of overlapping NGWFs according to

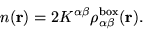$$n(\mathbf{r}) = 2K^{\alpha\beta}\rho_{\alpha\beta}^{\mathrm{box}}(\mathbf{r}).$$ (33)