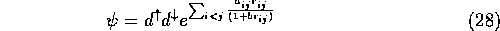
Optimising wavefunctions for use in QMC calculations is a relatively recent technique. It was pioneered by Umrigar [4] to calculate wavefunctions for use in VMC calculations on the Be atom. He took the standard atomic trial wavefunction
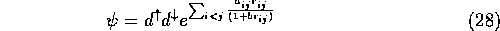
where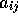 
is equal to 1/2 for antiparallel-spin electrons and 1/4
for parallel-spin electrons, to satisfy the cusp condition.
He then optimised the value of the parameter
b using a minimisation of variance technique. This technique and its
relative merits are discussed in detail in section 
.
He then generalised the Jastrow part of the wavefunction to take account of the individual positions of the electrons as well as the electron-electron separation.
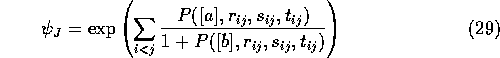
where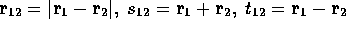 
and P is a complete 
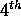order polynomial in r,s and t with
coefficients [a] and [b]. The coefficients [a] and [b] were then
optimised using the same minimisation of variance technique.
The error in the expectation value of the energy was reduced from 0.001
to 0.000003 Hartrees by the optimisation.
Mitas and Martin have also optimised wavefunctions for use in atomic QMC
calculations [5]. They also chose to use a 2 body correlation
function that depends on the electron-electron separation and the
electron-ion separation,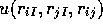 
.
where
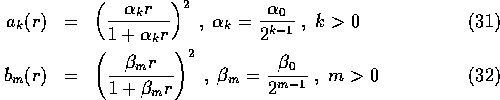
and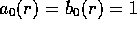 
.
The largest range of k,l,m used was from 0 to 5 but only a subset of
values were actually used.
When performing VMC calculations on atomic and molecular nitrogen
[6], Mitas and Martin used 21 variational parameters in
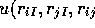. These were optimised in the VMC using the
Umrigar minimisation of variance technique.
Mitas and Martin have also begun optimising wavefunctions for use in
QMC calculations on solids. They used the same correlation
function () from the nitrogen atom calculations, but
with only 6 optimised parameters, to perform calculations on solid
nitrogen.
A few wavefunctions have also been generated by methods other than the Umrigar minimisation of variance technique [4]. Tanaka [7] has performed VMC calculations on the cohesive energy of NiO using wavefunctions generated by minimising the total energy of the wavefunction. He used a trial wavefunction where the Jastrow factor took its usual form
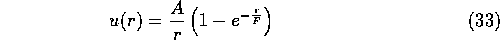
and the Chi function was expressed as a sum of Gaussians
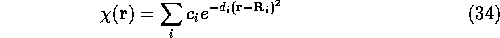
where 
is the electron position and 
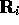is the position of
the ith ion.
In the cases of Mitas [5] and Tanaka [7] it is not possible to compare results before and after optimisation of parameters in the wavefunction as the optimisation scheme is used to generate the original parameters, rather than improve on a set of parameters that are already being used.
