Nick Woods

Nick Woods
Member of Clare College
PhD student in Dr Hasnip's group
Office: 543 Mott Bld
Phone: +44(0)1223 3 37466
Email: nw361 @ cam.ac.uk
ORCID: 0000-0002-5913-2206
TCM Group, Cavendish Laboratory
19 JJ Thomson Avenue,
Cambridge, CB3 0HE UK.
Research
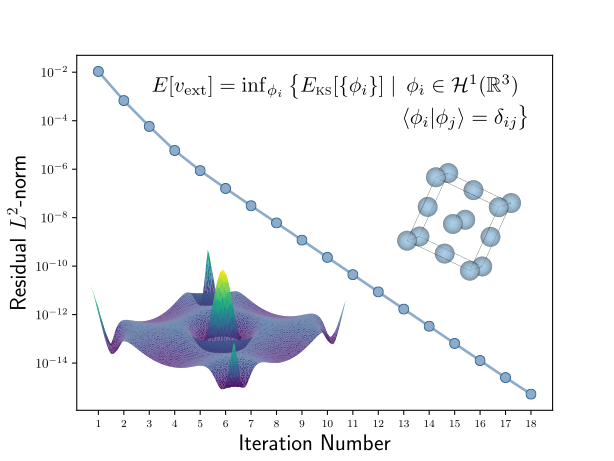
My research concerns the development and implementation of methodology utilised in computational implementations of Kohn-Sham density functional theory. However, this methodology is not strictly limited to Kohn-Sham theory, and my interests lie in all levels of electronic structure theory and their computational implementation.
In particular, my current research involves topics such as benchmarking self-consistency algorithms, exact calculation of various objects such as the Kohn-Sham effective potential, the density-density linear response function, the exchange-correlation kernel of linear response time-dependent density functional theory, and more.

In Plain English
Quantum mechanics is a theory -- a mathematical framework -- that has been exceptionally successful in describing and predicting natural phenomena. Hence, knowing the precise 'quantum mechanical' description of particles, the fundamental constituants of materials, provides a wealth of information about the material. For example, quantum mechanics is able to determine mechanical strength, opacity, electrical and thermal conductivity, and so on. Solving the equations of quantum mechanics in order to predict these properties is impossible in practice for realsitic materials. My research involves approximating the equations of quantum mechanics and refining the computational implementation of these approximations.Featured Publications
Insights from Exact Exchange-Correlation Kernels N. Woods, M. T. Entwistle, R. W. Godby Phys. Rev. B. 103, 125155 (2021)
Computing the Self-Consistent Field in Kohn-Sham Density Functional Theory N. Woods, P. Hasnip, M. C. Payne Journal of Physics: Condensed Matter, 31, 453001 (2019)
Algebraic Classical and Quantum Field Theory on Causal Sets E. Dable-Heath, C. J. Fewster, K. Rejzner, N. Woods Phys. Rev. D., 101, 065013 (2020) (Editors' suggestion)
On the Nature of Self-Consistency in Density Functional Theory N. Woods arXiv:1803.01763
Cosmological Predictions from the Primordial Universe: Non-Gaussianities N. Woods arXiv:1803.01759