Research Highlights
Non-Abelian Floquet braiding and anom- alous Dirac string phase in periodically driven systems
Predictions reveal a new class of topological phases that exist only in out of equilibrium.
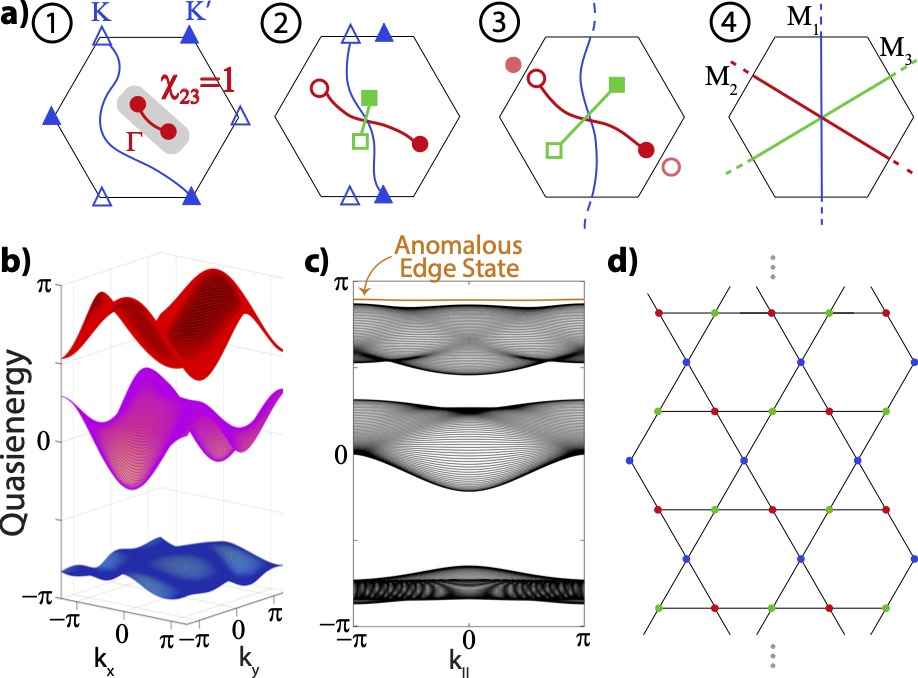
Realisation of an Anomalous Dirac string (ADS) phase when driving a Kagome model. The multi-gap topological configuration evolves as shown in steps 1-4 of panel a. The final stage entails the ADS phase, a new fully gapped phase with a Dirac string in each gap and a quasi-energy spectrum shown in panel b. Notably, the extra string of the anomalous gap signals an extra accumulation of Berry phase and thus an unconventional edge spectrum (panel c) for the ribbon geometry depicted in (d).
Reporting in Nature communications, we show that periodic (Floquet) driving can induce anomalous multi-gap topological properties that have no static counterpart. Multi-gap topologies are a new class of topological phases that have recently been discovered in static settings. We identify Floquet-induced non-Abelian braiding, which in turn leads to a phase characterized by an anomalous Euler class, being the prime example of a multi-gap topological invariant. Most strikingly,we also retrieve the first example of an ‘anomalous Dirac string phase’. This gapped out-of-equilibrium phase features an unconventional Dirac string configuration that physically manifests itself via anomalous edge states on the boundary. Our results not only provide a stepping stone for the exploration of intrinsically dynamical and experimentally viable multi-gap topological phases, but also demonstrate periodic driving as a powerful way to observe these non-Abelian braiding processes notably in quantum simulators.
Non-Abelian Floquet braiding and anomalous Dirac string phase in periodically driven systems, Robert-Jan Slager, Adrien Bouhon, F. Nur Ünal, Nature Communications 15, 1144 (2024).