Research Highlights
Machine learning for topological insulators
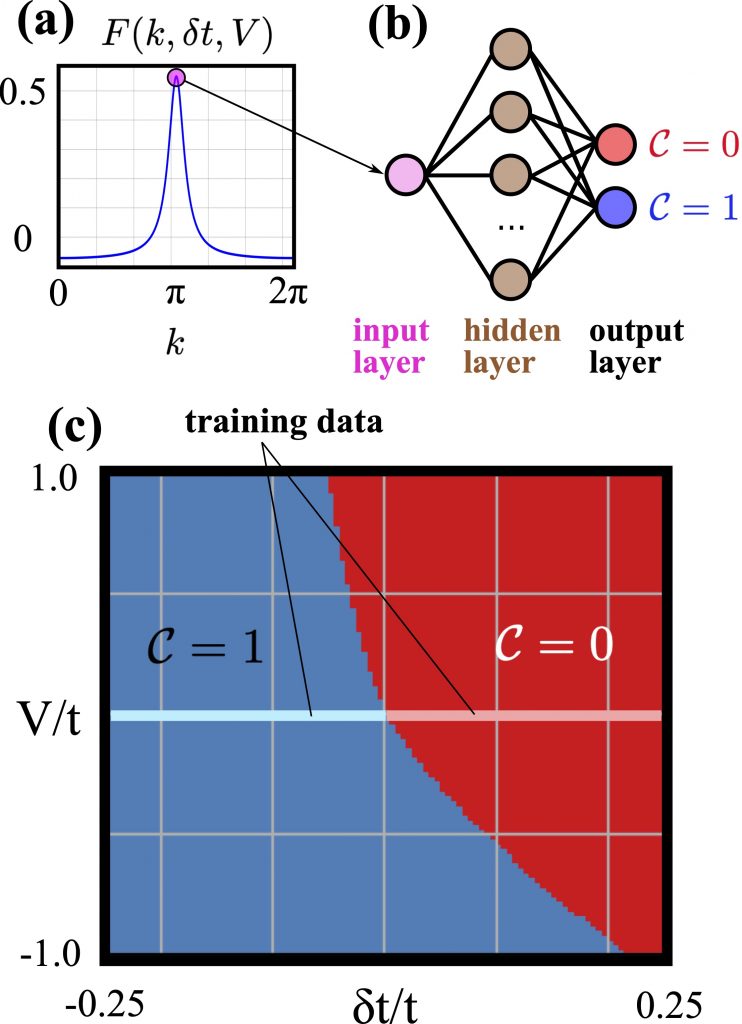
What is the minimal information required to describe something? It takes just two numbers to pinpoint any location on Earth – namely its longitude and latitude. It takes three numbers to generate any shade of color by using the RGB standard. And the famous idea of “six degrees of separation” purports that we only need six social connections to reach any given person on the planet.
But all these examples pertain to direct information. Things become fuzzier when we are dealing with quantities that are indirect, ie that cannot be pinpointed to a precise location, but emerge only after summing or averaging over many local instances. For example: what is the minimal amount of information necessary to recognize a human face? That’s a question that is relevant for both a portraitist and a face recognition software. Of course, we could simply take a picture and store all the pixels, but surely that’s redundant information. We can recognize facial features also in black and white photos. And sometimes we recognize people by their eyes only – specially in these covid-19 times where everyone is wearing a mask.
Another area where this question is relevant is topology. Topological materials have bizarre properties – such as being conducting on the edges while staying insulating in the bulk. These properties can be connected to a different topology of their electronic band structure, which can be summed up by a topological number or invariant. This invariant is a very nonlocal quantity. It is calculated by integrating a curvature function over all momentum space. In 3D systems or when we consider interactions – which add other dimensionalities to the calculation of the invariant – obtaining the full topological invariant can become very cumbersome. Furthermore, very often the curvature function is a rather localized object: it is highly-peaked at certain high-symmetry points, while it is negligible anywhere else. It seems thus that we do not really need to do the full integration to calculate the topological invariants approximatively.
This naturally prompts the question of what is the minimal information necessary to extract the topological invariants. In our new pre-print, we have addressed precisely this question in the context of topological insulators, leveraging on the power of machine learning. We have discovered that it is enough to use only the value of the curvature function at the high-symmetry points as input to determine the topological invariant and correctly delineate the topological phase diagram of various topological insulators in 1D and 2D. We can train a simple neural network with this data, and it automatically learns how to recognize different topological phases.
The machine learning algorithm can also go one step further. We can train the neural network with data from noninteracting topological insulators (which are typically much easier to handle), and then apply the trained machine to interacting topological insulators. Despite the presence of interactions and the more complicated form of the curvature function, the algorithm is still able to correctly identify all the topological phases and phase transitions with a sizeable speed-up in computation time. This speed-up allowed us to probe a larger parameter space and discover new results, such as the appearance of multicriticality induced by the interactions.
So, in this case, it looks like the minimal information necessary to describe topological insulators is just one single number at each high-symmetry point.
A supervised learning algorithm for interacting topological insulators based on local curvature Paolo Molignini, Antonio Zegarra, Evert van Nieuwenburg, R. Chitra, Wei Chen SciPost Phys. 11, 073 (2021)