Research Highlights
Majoranas across dimensions
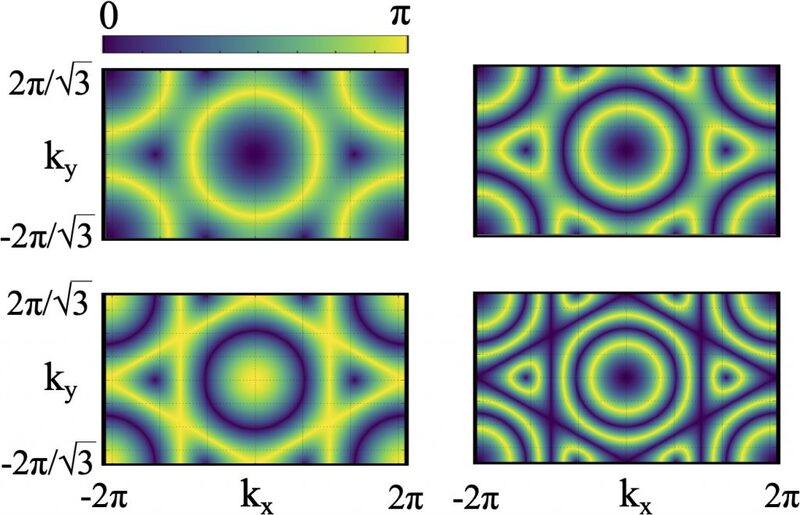
The famous Dutch painter Piet Mondrian once said that “Dimension can exist only through other dimensions”. This seems to be indeed true for a certain paradigmatic model of condensed matter physics known as the Kitaev model, where topological phase transitions reflect different dimensionalities than the ones we expect.
The Kitaev model describes spins on a two-dimensional (2D) honeycomb lattice and is famous because it hosts collective excitations known as Majorana modes — the condensed-matter cousins of the elusive particle postulated in 1937 by Ettore Majorana as a solution of the Dirac equation in particle physics but yet to be discovered in the wild. Majorana modes have outlandish properties. They are purely real and their own antiparticle. They localise at the edges of finite-size sample. And they belong to the class of nonabelian anyons: by moving two of such particles around each other, one does not go back to the initial configuration, but creates a very stable topological braiding which could be used to encode quantum information.
In our paper, we discover more intriguing properties associated with changes in the number of Majorana modes in the Kitaev model. When Majorana modes are created or destroyed, the system undergoes a topological phase transition. These phase transitions can be classified in universality classes by looking at how certain quantities behave (usually they diverge with a certain power law) as the transition takes place. The universality class is described by a set of critical exponents that encode among other things the dimensionality of the phase transition. In the static Kitaev model, despite being defined on a 2D lattice, we surprisingly find that the critical exponents describe a universality class expected for 1D systems! It therefore seems that the model behaves more like a 1D system rather than a 2D one.
Once we modulate parameters in time, things become even more exotic. The Majorana modes become chiral and start propagating along the edges of the 2D sample. The corresponding topological phase transitions then revert to being truly two-dimensional. But there is more! As a function of the driving parameters, we discover a special regime where the dynamics is momentarily frozen. At this point, we encounter an additional type of topological phase transition: a transition to a nodal-loop semimetal phase. The name of the phase comes from the properties of the electronic bands, that touch along closed loops. This is in contrast to what happens for the bands of the topological phase transitions associated with the chiral Majorana modes, which close at single points. In the nodal-loop semimetal phase, the Majorana modes revert to being static. Furthermore, because the loops are 1D structures, the dimensionality of this phase transition is again reduced to 1D. It turns out that the nodal loop semimetal phase appears because of emergent time-reversal and mirror symmetries that are generated by the driving procedure. By carefully tuning in and out of this phase, we have a way of controlling the propagation direction and velocity of the chiral Majorana modes.
Coming back to Mondrian’s citation, it is rather fitting that the nodal loops -with their “dimensions within a dimension” — are reminiscent of the bright and geometric shapes painted by the Dutch artist (see image below).
Crossdimensional universality classes in static and periodically driven Kitaev models, Paolo Molignini, Albert Gasull Celades, R. Chitra, and Wei Chen Phys. Rev. B 103, 184507 (2021)