Research Highlights
Wigner Formulation of Thermal Transport in Solids
Two different microscopic mechanisms for heat transport are known in solids. In crystals, heat carriers behave akin to particles in a gas, whereas in glasses, heat transfer bears analogies to the physics of waves. This paper elucidates how quantum wave-particle duality emerges in thermal transport, discussing how particlelike and wavelike heat-transport mechanisms can emerge and coexist, and providing a quantitative criterion to assess their relative strength and the crossover between the regimes where one or the other dominates.
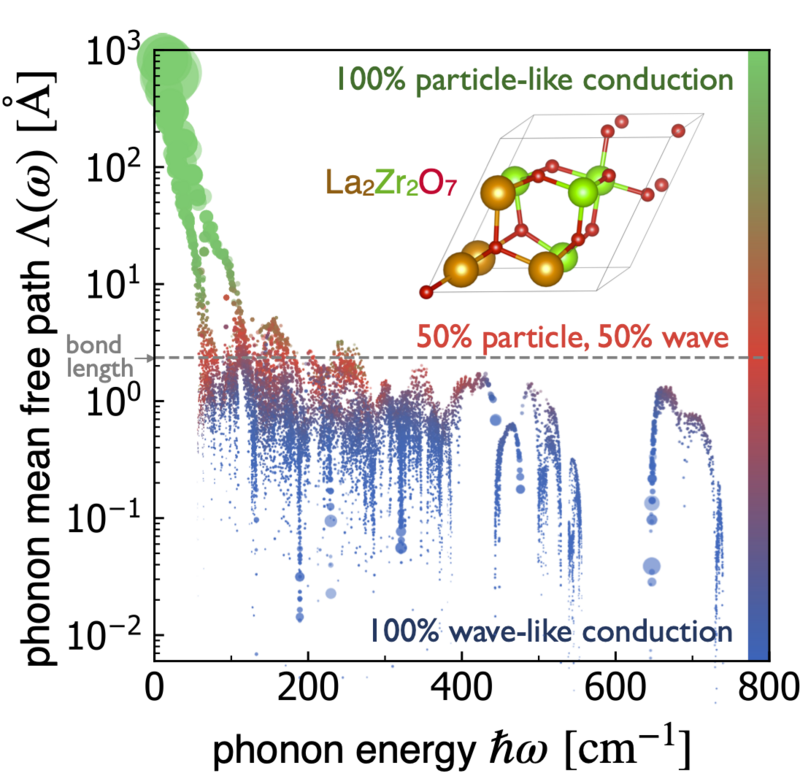
In 1929, Peierls formulated the phonon Boltzmann transport equation to explain heat conduction in crystalline solids, discussing how quantized atomic vibrations mediated heat transport. This formulation successfully explained the temperature-conductivity curve observed in good thermal conductors with crystalline structure but could not describe glasses or low thermal conductors. In 1989, Allen and Feldman made a key step forward on the description of thermal transport in glasses, envisioning that in glasses, atomic vibrations with very similar energies can interfere constructively, enabling a wavelike tunneling mechanism through which heat can propagate.
In this work, we discuss the theoretical foundations of a “Wigner” heat-transport equation (named after the Wigner formulation of quantum mechanics used to derive it) that naturally encompasses the coexistence of particlelike and wavelike conduction mechanisms, unifying and extending the Peierls and Allen-Feldman formulations. We discuss the conditions determining the relative strength of particlelike and wavelike conduction mechanisms, showing that in the intermediate case of complex crystals with ultralow thermal conductivity these can be equally relevant.
Our findings pave the way for the theory-driven optimization of thermal barriers and thermoelectrics, since in these materials it is crucial to account for heat’s particle-wave duality to correctly describe the thermal conductivity.
Wigner formulation of thermal transport in solids. Phys. Rev. X 12 041011 (2022)