Research Highlights
DMRG for quantum systems in the continuum
Researchers develop framework for calculating the properties of strongly interacting quantum systems in new regimes.
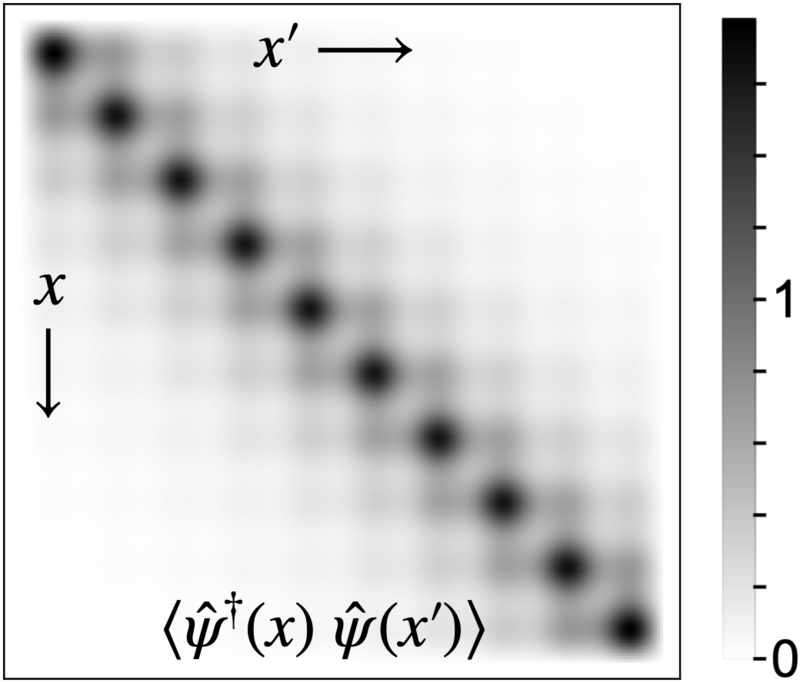
Spatial correlations for 10 strongly interacting bosons in a box, subject to a shallow lattice potential with 10 equally spaced minima. The correlations decay exponentially with separation, characteristic of a Mott insulator. The ground state was obtained by dividing the box into 20 segments.
Simulating a quantum system on a classical computer is hard, as the number of possible quantum states grows exponentially with the number of particles. For systems on a lattice, the "Density-Matrix Renormalisation Group" (DMRG) provides a solution by letting one judiciously truncate this space based on the entanglement between subsystems, making it the current state of the art in low dimensions. However, in the continuum there are infinitely many quantum states even for a single particle. Thus, an extension of DMRG has proved elusive, particularly for inhomogeneous or time-dependent settings.
The authors introduce a new approach, called cDMRG, that can overcome this long-standing challenge. They divide space to map a continuous system to a discrete sum over segments, each with a flexible set of basis functions to describe the local many-body state. By combining this map with existing DMRG routines, one can accurately obtain physical quantities directly in the continuum. As in lattice DMRG, one quickly converges to the ground state in both homogeneous and inhomogeneous settings. The method can be tailored to a wide range of physical systems and generalised for time evolution.
This study opens up DMRG and other tensor-network techniques for tackling challenging problems in the continuum.
Shovan Dutta, Anton Buyskikh, Andrew Daley, Erich Mueller, Phys. Rev. Lett. 128 230401 (2022).
An open-source code is available on GitHub.