Research Highlights
Charged surfaces and 3D periodicity
Many codes can calculate solutions of Schrödinger's equation for a range of different materials. Once solved, many chemical and material properties can be accurately predicted. Codes designed to work on solids tend to assume that the material is periodic in all three dimensions. This causes problems if the system is charged; the energy per unit volume becomes infinite.
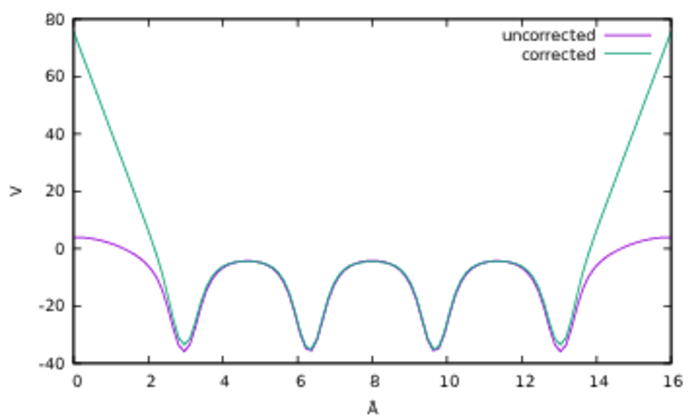
Surfaces can be studied in such codes by forming an infinite sandwich of alternating layers of bulk and vacuum. Whilst removing the infinity from the energy is easy, obtaining rapid convergence of the energy, potential, or charge density with vacuum separation is less easy. Large amounts of vacuum can be very computationally expensive.
This paper reviews some of the existing correction schemes, and presents a novel technique for achieving rapid convergence and accurate results. The correction described is self-consistent, and for some properties can reduce the computational time needed for a given accuracy by more than a factor of twenty compared to non self-consistent corrections.
Charged surfaces and slabs in periodic boundary conditions Electronic Structure 3 015002 (2021)