Research Highlights
A new diagnostic for quantum chaos
A new probe of quantum chaos is orders of magnitude more sensitive than standard measures and can extract information about the nontrivial dynamics close to nonchaotic regimes.
A schematic representation of the eigenstate sensitivity to chaos-inducing perturbations.
Quantum chaos and ergodicity, which underlies all of statistical mechanics and thermodynamics, manifests itself in a vast range of phenomena. While researchers have developed powerful mathematical tools for understanding the emergence of chaos in quantum systems, the same cannot be said for probes that verify that the system is indeed chaotic. Although standard measures of quantum chaos exist, they are generally not very sensitive. We propose a sensitive probe for quantum chaos that is in line with both quantum and classical definitions of chaos.
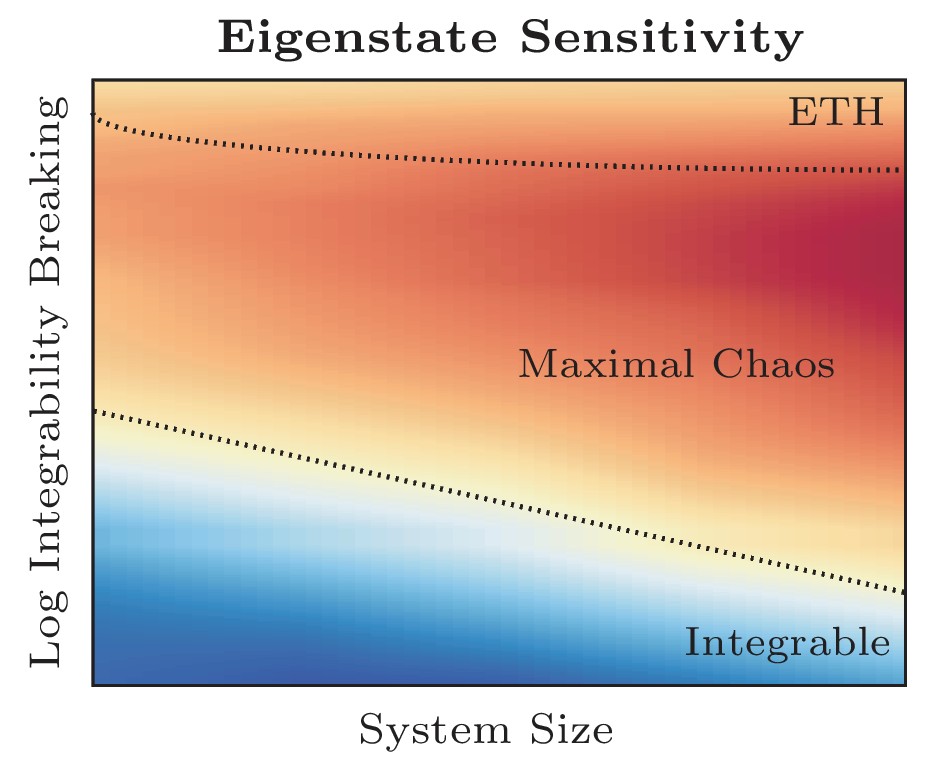
To understand the emergence of chaos in quantum systems, researchers rely on the eigenstate thermalization hypothesis. Briefly, the hypothesis says that quantum chaos is encoded in the set of allowed energy states of a quantum system, as opposed to classical chaos which is expressed through exponential sensitivity of particle trajectories to initial conditions. Our proposed probe of quantum chaos blends both definitions by quantifying the sensitivity of allowed energy states to small perturbations. Using an appropriate measure, we can detect quantum chaos orders of magnitude before standard measures and extract information about nontrivial dynamics close to nonchaotic regimes. We use this probe to establish the existence of a regime separating nonchaotic and chaotic systems, characterized by a maximal sensitivity of allowed energy states and anomalously slow (exponentially long) relaxation times.
This work shows that there is a maximally susceptible regime separating chaotic and nonchaotic systems. Our measure can probe this regime, which is completely invisible to standard measures such as level-spacing statistics.
Mohit Pandey, Pieter W. Claeys, David K. Campbell, Anatoli Polkovnikov, and Dries Sels, Phys. Rev. X 10, 041017 (2020)