Research Highlights
Novel braiding properties in momentum space and topology discovered in a general class of metals
Researchers uncover new topological charges in specific kinds of metals
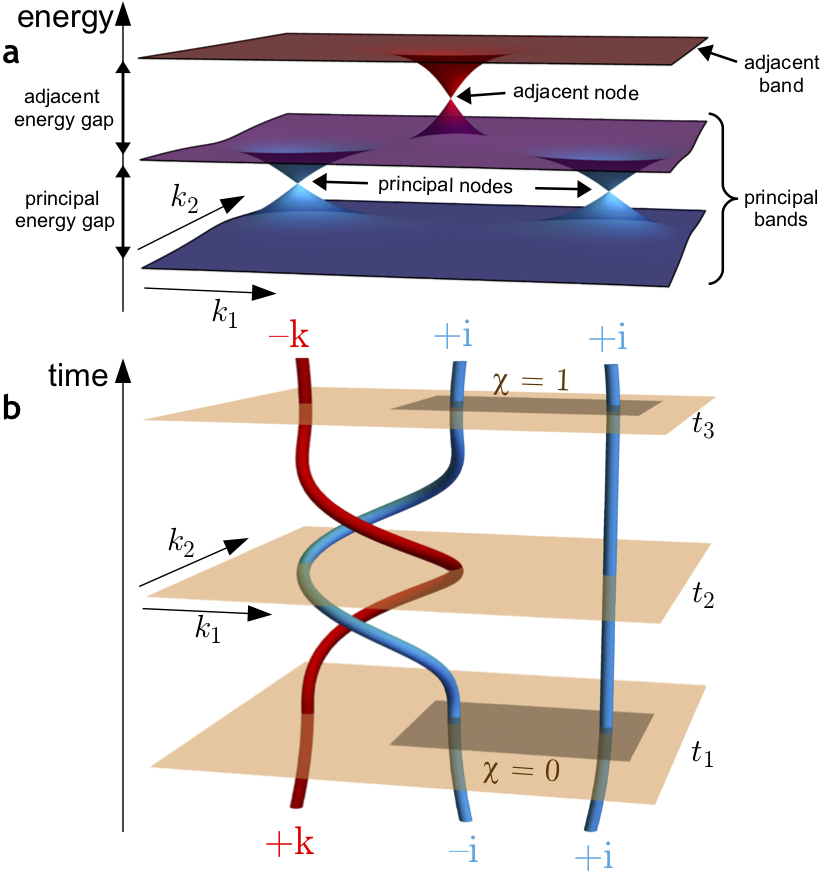
Reciprocal braiding of band nodes-. We inspect the ability of the ``principal'' nodes, assumed to be near the Fermi level, to pairwise annihilate. Considering two ``principal'' bands that form nodes (blue), and a third ``adjacent'' band which enables additional species of band nodes (red) formed by the unoccupied bands. b.) By adjusting the Hamiltonian parameters as a function of time (orange planes), the node trajectories form braids in the momentum space. The braid converts topological charges of the nodes (indicated by quaternion numbers) and affects their ability to pairwise annihilate. We find that the same property is encoded using Euler class, which changes value on the dark region during the braiding process.
Topology is branch of mathematics that studies and classifies properties that are invariant under smooth deformations. A paradigmatic example is the relation between a doughnut and a coffee cup; one can be deformed into the other making them topologically speaking the same, which can be roughly quantified by analysing the number of holes of both objects. Topological quantities have transformed the field of physics the past few decades as it turns out that many phases of matter can be understood by such evaluations. These characterisations are inherently robust as, by definition, they are insensitive to local details. In this work we find that there is a general class of metallic materials that, due to presence of symmetry, allow for a specific kind of topological description. Apart from retrieving relations with intricate mathematical evaluations, this study reveals that such systems host band node excitations with new kinds of charges that can be altered by non-local actions; when these excitations are braided around each other in momentum space they change character. In fact, the topology of the underlying system can be understood as consequence of these intricate braiding processes and hence could in principle also be manipulated to store data. Finally, the general descriptive nature of the work can be employed to evaluate specific candidate materials and accordingly a few specific realisations are predicted.
Non-Abelian Reciprocal Braiding of Weyl Points and its Manifestation in ZrTe Adrien Bouhon, QuanSheng Wu, Robert-Jan Slager,Hongming Weng, Oleg Yazyev and Tomas Bzdusek, Nature Physics (2020)