Research Highlights
Exhaustive framework describing boundary modes of open quantum systems discovered
The authors retrieve a generic famework to enmerate boundary modes in open quantum systems
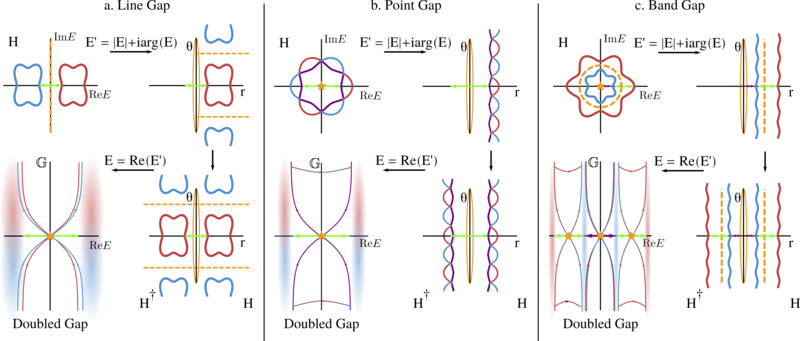
Non-Hermitian gap topology.Top rows illustrate a mapping of non-Hermitian bands on the punctured complex plane to a strip. Systems are then duplicated along the right column of each panel. Bands are collapsed to real line in bottom rows, and we plot in-gap doubled Green’s functions across different band gaps (orange markers) with blue-red smears representing Bloch bands. Curves crossing the gap depict a topological example of in-gap doubled Green’s function G eigenvalues. A line gap (a) protects zeros of G crossing from red (blue) to blue (red) bands, while bands in (c) may have both point gap invariants (crossing zero in purple gap) and band gap invariants (red to blue).
We consider conditions for the existence of boundary modes in non-Hermitian systems with edges of arbitrary codimension. Through a universal formulation of formation criteria for boundary modes in terms of local Green’s functions, we outline a generic perspective on the appearance of such modes and generate corresponding dispersion relations. In the process, we explain the skin effect in both topological and nontopological systems, exhaustively generalizing bulk-boundary correspondence to different types of non-Hermitian gap conditions, a prominent distinguishing feature of such systems. Indeed, we expose a direct relation between the presence of a point gap invariant and the appearance of skin modes when this gap is trivialized by an edge. This correspondence is established via a doubled Green’s function, inspired by doubled Hamiltonian methods used to classify Floquet and, more recently, non-Hermitian topological phases. Our work constitutes a general tool, as well as a unifying perspective for this rapidly evolving field. Indeed, as a concrete application we find that our method can expose novel non-Hermitian topological regimes beyond the reach of previous methods.
Non-Hermitian Boundary Modes and Topology D.S. Borgnia, A. J. Kruchkov and R.-J. Slager, Phys. Rev. Lett. 124 056802 (2020)