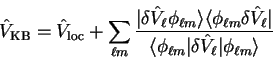Next: 5.7 Computational implementation
Up: 5. Localised basis-set
Previous: 5.5 Kinetic energy matrix
Contents
Subsections
In this section we present two methods for obtaining the non-local
pseudopotential matrix elements. The first constructs a Green's function
in order to expand the basis functions on one site in terms of the
same functions centred elsewhere. This method is particularly efficient,
although it requires some restrictions to be made in the radial part of
the support functions to give a variational method. The second method
adopts the Kleinman-Bylander form and uses the results for the
overlap matrix elements. This method is slower, but more robust numerically
and allows direct comparison with existing pseudopotential codes.
5.6.1 Green's function method
The general form for a semi-local pseudopotential operator (i.e. one
which is non-local in the angular but not radial coordinates) for an
ion is
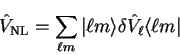 |
(5.30) |
where
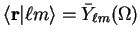 and
and
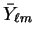 is centred on the ion.
is centred on the ion.
The pseudopotential components
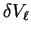 are themselves
short-ranged in real-space, and vanish beyond the core radius
are themselves
short-ranged in real-space, and vanish beyond the core radius
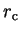 . Therefore the action of the non-local
pseudopotential depends only upon the form of the wave-functions
within this core region. We require the matrix elements of the
non-local pseudopotential between localised basis functions which are
not necessarily centred on the ion.
. Therefore the action of the non-local
pseudopotential depends only upon the form of the wave-functions
within this core region. We require the matrix elements of the
non-local pseudopotential between localised basis functions which are
not necessarily centred on the ion.
We therefore need to find an expansion of the basis functions in
terms of functions localised within the pseudopotential core. Since
the basis functions are all solutions of the Helmholtz equation, we
invoke the uniqueness theorem which states that the expansion we seek
is uniquely determined by the boundary conditions on the surface of
the core region and solve the Helmholtz equation subject to these
inhomogeneous boundary conditions by the standard method using the
formal expansion of the Green's function.
We can write the basis function over all space using the Heaviside step
function 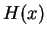
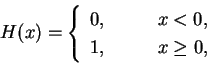 |
(5.31) |
so that a basis function centred in a sphere of radius 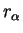 at
the origin (i.e. for
at
the origin (i.e. for
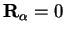 ) is
) is
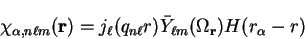 |
(5.32) |
and therefore
![\begin{displaymath}
(\nabla^2 + q_{n \ell}^2) \chi_{\alpha , n \ell m}({\bf r}) ...
...elta(r_{\alpha}-r) \right] {\bar Y}_{\ell m}(\Omega_{\bf r}) .
\end{displaymath}](img730.gif) |
(5.33) |
The terms on the right-hand side only contribute on the sphere boundary
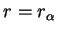 ; everywhere else in space the basis function obeys the
homogeneous Helmholtz equation (5.1). These terms will give
rise to an extra term in the Green's function solution due to the
discontinuity of the first radial derivative of the basis function at the
sphere boundary. However, if the radial function for each angular
momentum component has a continuous first derivative, then these
contributions will cancel. In this case, we can proceed assuming that the
basis function obeys the homogeneous equation everywhere.
This condition is naturally obeyed by the
support functions when the support regions are large enough, since there is
a kinetic energy penalty associated with the same discontinuity in the
radial wave-function, but in this case we would lose any variational
principle if there was a discontinuity at any stage during the minimisation.
A better solution is to impose a sum rule on the expansion coefficients in
equation 5.3 to maintain a continuous radial derivative i.e.
; everywhere else in space the basis function obeys the
homogeneous Helmholtz equation (5.1). These terms will give
rise to an extra term in the Green's function solution due to the
discontinuity of the first radial derivative of the basis function at the
sphere boundary. However, if the radial function for each angular
momentum component has a continuous first derivative, then these
contributions will cancel. In this case, we can proceed assuming that the
basis function obeys the homogeneous equation everywhere.
This condition is naturally obeyed by the
support functions when the support regions are large enough, since there is
a kinetic energy penalty associated with the same discontinuity in the
radial wave-function, but in this case we would lose any variational
principle if there was a discontinuity at any stage during the minimisation.
A better solution is to impose a sum rule on the expansion coefficients in
equation 5.3 to maintain a continuous radial derivative i.e.
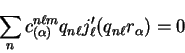 |
(5.34) |
which can be used to fix one coefficient in terms of the rest for each
angular momentum component. This is the
restriction mentioned above which must be imposed if the Green's function
method is to be used.
The basis function is assumed to obey the homogeneous Helmholtz equation
throughout all space. In the original support region, homogeneous
boundary conditions were applied. Now, in an overlapping region of radius
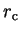 (the core region for the non-local pseudopotential), the
basis function must still obey the same homogeneous Helmholtz equation, but it
is now subject to inhomogeneous boundary conditions. Standard
methods can be used to transform this problem into the solution of
an inhomogeneous Helmholtz equation subject to homogeneous boundary conditions,
and this new problem has a standard solution in terms of the Green's function,
which can be formally expanded in terms of the eigenfunctions of an
appropriate self-adjoint operator (here the operator on the left of the
Helmholtz equation).
The result is
(the core region for the non-local pseudopotential), the
basis function must still obey the same homogeneous Helmholtz equation, but it
is now subject to inhomogeneous boundary conditions. Standard
methods can be used to transform this problem into the solution of
an inhomogeneous Helmholtz equation subject to homogeneous boundary conditions,
and this new problem has a standard solution in terms of the Green's function,
which can be formally expanded in terms of the eigenfunctions of an
appropriate self-adjoint operator (here the operator on the left of the
Helmholtz equation).
The result is
![\begin{displaymath}
\chi_{\alpha , n \ell m}({\bf r}) = \sum_{\ell' m'} f_{\ell'...
...(q_{n'
\ell'} r') \right] {\bar Y}_{\ell' m'}(\Omega_{\bf r'})
\end{displaymath}](img732.gif) |
(5.35) |
and is valid for points
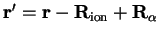 within the core region (i.e. for
within the core region (i.e. for
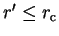 ).
).
The coefficients
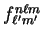 and
and
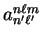 are defined by:
are defined by:
The
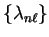 are chosen by
are chosen by
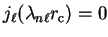 and play the same rôle as the
and play the same rôle as the
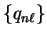 in the expansion of the wave-functions. The integral in
equation 5.37 is straightforward to evaluate for
given
in the expansion of the wave-functions. The integral in
equation 5.37 is straightforward to evaluate for
given 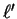 .
.
The surface integral in equation 5.36 is evaluated
by first rotating the coordinate system so that the new 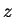 -axis is
parallel to
-axis is
parallel to
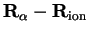 , thus mixing
the spherical harmonics [151]. The elements of the
orthogonal spherical harmonic mixing matrices
, thus mixing
the spherical harmonics [151]. The elements of the
orthogonal spherical harmonic mixing matrices
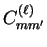 are
defined by the elements of the rotation matrix for the coordinate
system. In terms of the components
are
defined by the elements of the rotation matrix for the coordinate
system. In terms of the components 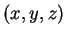 of the vector
of the vector
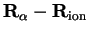 of length
of length
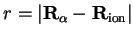 , and
, and 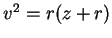 ,
the rotation matrix
,
the rotation matrix 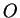 is given by:
is given by:
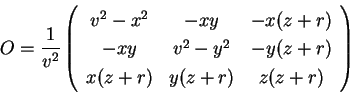 |
(5.37) |
The singularity which occurs when 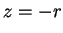 i.e. when the ion is ``vertically''
above the support region, is avoided by inverting the calculation through
the origin when
i.e. when the ion is ``vertically''
above the support region, is avoided by inverting the calculation through
the origin when 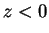 .
The spherical harmonic matrices
.
The spherical harmonic matrices
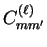 can be written in terms
of the elements of this matrix. Here we write them out explicitly for
can be written in terms
of the elements of this matrix. Here we write them out explicitly for  :
:
In the new coordinate system, the surface integral is written
in terms of a one-dimensional integral
in which the dimensionless variable
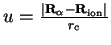 is
introduced.
is
introduced.
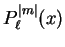 denotes an associated Legendre
polynomial, and these integrals can all be calculated indefinitely
using elementary methods once the integrand is expanded into
trigonometric functions.
denotes an associated Legendre
polynomial, and these integrals can all be calculated indefinitely
using elementary methods once the integrand is expanded into
trigonometric functions.
Figure 5.2:
Non-local pseudopotential energy against number of
Bessel functions used in Green's function expansion
|
|
The numerical evaluation of the analytic results for
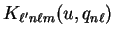 is inaccurate when
is inaccurate when 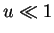 and in this
case it is necessary to employ Taylor expansions of the results. The two
different cases for the upper limit of the integral also need to be
treated separately, and this is one reason why the Kleinman-Bylander method
described next is preferred.
and in this
case it is necessary to employ Taylor expansions of the results. The two
different cases for the upper limit of the integral also need to be
treated separately, and this is one reason why the Kleinman-Bylander method
described next is preferred.
The final result for
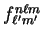 is then
is then
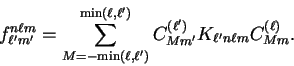 |
(5.41) |
Defining the core matrix elements
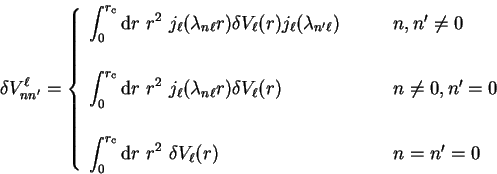 |
(5.42) |
the matrix element of the non-local pseudopotential operator between
any two basis functions overlapping the core (
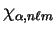 and
and
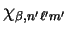 ) can be written (defining
) can be written (defining
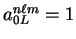 ) as the sum:
) as the sum:
The non-local pseudopotential data is therefore stored in terms of the
core matrix elements defined in equation 5.45. In figure
5.2 we plot the non-local pseudopotential energy against
the number of core Bessel functions for an s-local silicon
pseudopotential generated according to the scheme of Troullier and
Martins [74]. We see that the energy converges
rapidly with the number of core Bessel functions used (the dashed line
is the energy calculated with fifty core functions.) Increasing the
number of core functions only increases the number of
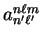 coefficients required, and the separable nature of the
calculation means that even using fifty core functions requires very
little computational effort.
coefficients required, and the separable nature of the
calculation means that even using fifty core functions requires very
little computational effort.
5.6.2 Kleinman-Bylander form
Figure 5.3:
Non-local pseudopotential energy against number of
Bessel functions used to describe Kleinman-Bylander projectors.
|
|
We reproduce equation 3.76 which demonstrates the
Kleinman-Bylander form of the pseudopotential in terms
of pseudo-atomic eigenstates
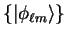 .
.
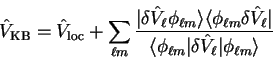 |
(5.44) |
For pseudopotentials whose non-local components
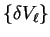 vanish at the
core radius
vanish at the
core radius 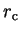 , the projector states
, the projector states
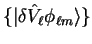 can be expanded
in the basis-states
can be expanded
in the basis-states
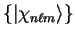 , and then the
matrix-elements of the pseudopotential operator are straightforwardly
obtained by applying the result for the overlap matrix elements, without
resorting to the scheme by King-Smith et al. [152].
, and then the
matrix-elements of the pseudopotential operator are straightforwardly
obtained by applying the result for the overlap matrix elements, without
resorting to the scheme by King-Smith et al. [152].
In figure 5.3 we show how the non-local pseudopotential energy
rapidly converges as the number of Bessel functions used to expand the
Kleinman-Bylander projectors is increased. This method is numerically
more stable than the Green's function method, although slower,
and has the added advantage that it allows a direct comparison to be made
between the results calculated using this basis-set and traditional
plane-wave codes. For these reasons the Kleinman-Bylander method has
been used in computational implementations.




Next: 5.7 Computational implementation
Up: 5. Localised basis-set
Previous: 5.5 Kinetic energy matrix
Contents
Peter Haynes
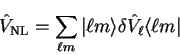
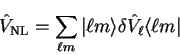
![]() are themselves
short-ranged in real-space, and vanish beyond the core radius
are themselves
short-ranged in real-space, and vanish beyond the core radius
![]() . Therefore the action of the non-local
pseudopotential depends only upon the form of the wave-functions
within this core region. We require the matrix elements of the
non-local pseudopotential between localised basis functions which are
not necessarily centred on the ion.
. Therefore the action of the non-local
pseudopotential depends only upon the form of the wave-functions
within this core region. We require the matrix elements of the
non-local pseudopotential between localised basis functions which are
not necessarily centred on the ion.
![]()
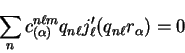
![\begin{displaymath}
\chi_{\alpha , n \ell m}({\bf r}) = \sum_{\ell' m'} f_{\ell'...
...(q_{n'
\ell'} r') \right] {\bar Y}_{\ell' m'}(\Omega_{\bf r'})
\end{displaymath}](img732.gif)
![]() and
and
![]() are defined by:
are defined by:
![]() -axis is
parallel to
-axis is
parallel to
![]() , thus mixing
the spherical harmonics [151]. The elements of the
orthogonal spherical harmonic mixing matrices
, thus mixing
the spherical harmonics [151]. The elements of the
orthogonal spherical harmonic mixing matrices
![]() are
defined by the elements of the rotation matrix for the coordinate
system. In terms of the components
are
defined by the elements of the rotation matrix for the coordinate
system. In terms of the components ![]() of the vector
of the vector
![]() of length
of length
![]() , and
, and ![]() ,
the rotation matrix
,
the rotation matrix ![]() is given by:
is given by:
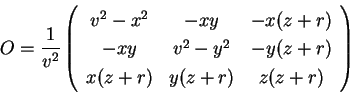
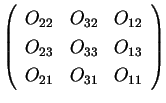
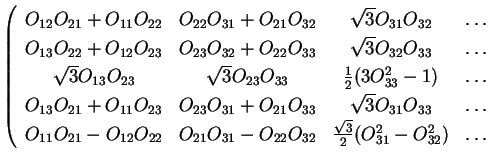
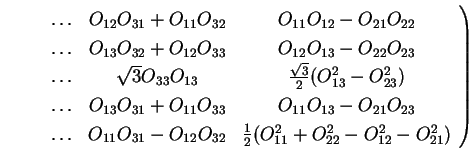
![$\displaystyle K_{\ell' n \ell m}(u,q_{n \ell}) = \frac{1}{2 u} \left[ (2 \ell' ...
...t)!}{(\ell' + \vert m\vert)!
(\ell + \vert m\vert)!} \right]^{1 \over 2} \times$](img760.gif)
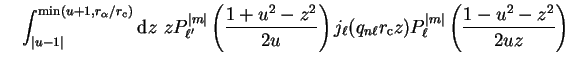
![\includegraphics [height=100mm,angle=-90]{nlplot.eps}](img764.gif)
![]() is inaccurate when
is inaccurate when ![]() and in this
case it is necessary to employ Taylor expansions of the results. The two
different cases for the upper limit of the integral also need to be
treated separately, and this is one reason why the Kleinman-Bylander method
described next is preferred.
and in this
case it is necessary to employ Taylor expansions of the results. The two
different cases for the upper limit of the integral also need to be
treated separately, and this is one reason why the Kleinman-Bylander method
described next is preferred.
![]() is then
is then
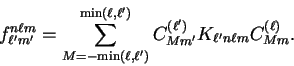
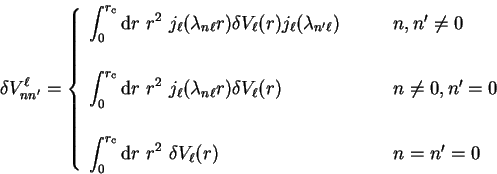
![\includegraphics [height=100mm,angle=-90]{nlplot2.eps}](img772.gif)