



Next: 4.6 Non-orthogonal orbitals
Up: 4. Density-Matrix Formulation
Previous: 4.4 Constraints on the
Contents
Subsections
We have shown how it is possible to reformulate density-functional theory in
terms of the single-particle density-matrix, and the constraints which must
be obeyed by ground-state density-matrices. However, in the coordinate
representation, we note that the density-matrix is a function of two position
variables
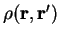 and thus contains an amount of information
which scales as the square of the system-size (as of course it must since
it contains all of the information in the Kohn-Sham orbitals, which are
functions of one position but with the number of occupied orbitals also scaling
linearly with system-size). To obtain a linear-scaling method, it is necessary
to impose some further restrictions on the density-matrix.
and thus contains an amount of information
which scales as the square of the system-size (as of course it must since
it contains all of the information in the Kohn-Sham orbitals, which are
functions of one position but with the number of occupied orbitals also scaling
linearly with system-size). To obtain a linear-scaling method, it is necessary
to impose some further restrictions on the density-matrix.
4.5.1 Separability
In practice we do not wish to deal with a function of six variables (i.e. two
three-dimensional positions).
From the factorisation property of idempotent density-matrices, or the
definition of the ground-state density-matrix in terms of the Kohn-Sham
orbitals;
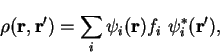 |
(4.58) |
we see that it is possible to consider separable density-matrices described
in terms of some auxiliary orbitals. The general form of a separable
density-matrix in terms of orbitals
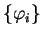 is
is
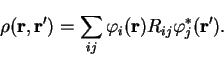 |
(4.59) |
Although it is not necessary for the auxiliary orbitals to be orthonormal, in the
case when they are, we can consider this general form as simply a
unitary transformation of the Kohn-Sham expression (4.58):
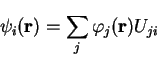 |
(4.60) |
where 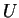 is the unitary matrix which diagonalises
is the unitary matrix which diagonalises 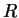 :
:
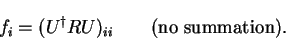 |
(4.61) |
When the auxiliary orbitals are not orthonormal, then they can be viewed as a
more general linear combination of the Kohn-Sham orbitals (involving both a
unitary and Löwdin transformation) which is described in
section 4.6. Whichever case applies, there is no loss of
generality here as all idempotent matrices can always be expressed in this way,
and these are the density-matrices of interest to us.
Kohn [136] has proved that in one-dimensional systems with a gap,
a set of exponentially decaying Wannier functions can be found in the tight-binding limit, and that this localisation is related to the square-root of the gap.
His method is not easily generalised to higher numbers of dimensions, and so until recently the exact nature of the Wannier functions in general three-dimensional systems was unknown, although it was anticipated that they would decay exponentially [137,138,139]. More recent numerical and analytical studies of the localisation of the density-matrix showed the decay to be exponential and again related to the square-root of the gap [140,141], thus supporting the general validity of Kohn's result. Very recently, however, Ismail-Beigi and Arias [142] have argued that in the weak-binding limit the exponential decay varies linearly with the gap. What is now certain is that the Wannier functions and density-matrix decay exponentially in systems with a gap, and that this decay is more rapid in systems with larger gaps.
Wannier functions
are simply a unitary transformation of Bloch wave-functions with respect to
the complementary variables of Bloch wave-vector and lattice vector.
Let
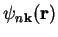 be
the normalised Bloch wave-function for the
be
the normalised Bloch wave-function for the 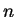 th band with wave-vector
th band with wave-vector
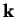 . Then the corresponding Wannier function for that band
. Then the corresponding Wannier function for that band
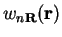 is defined by [143]
is defined by [143]
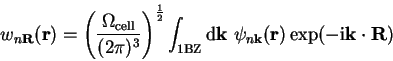 |
(4.62) |
and naturally the inverse relation holds:
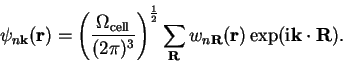 |
(4.63) |
The properties of Wannier functions are that they are localised in different
cells (labelled by lattice vector  ) and
are orthonormal:
) and
are orthonormal:
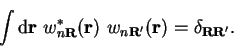 |
(4.64) |
The single-particle density-matrix in the case of full 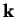 -point sampling
-point sampling
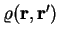 is given by
is given by
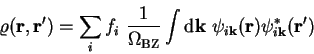 |
(4.65) |
(in which we have assumed that we are dealing with an insulator with completely
full or empty bands) which is a trace over wave-vector 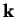 and thus
invariant under unitary transformation so that it can also be written
and thus
invariant under unitary transformation so that it can also be written
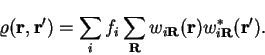 |
(4.66) |
Thus if the Wannier function
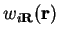 is vanishing when
is vanishing when
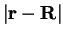 is large, then when
is large, then when
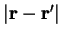 is large the
density-matrix must also vanish in the same way since it is impossible in that
case for both
is large the
density-matrix must also vanish in the same way since it is impossible in that
case for both
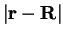 and
and
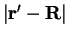 to be small.
Thus we expect that
to be small.
Thus we expect that
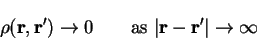 |
(4.67) |
where at zero temperature the decay is exponential in insulators and algebraic in metals.
We can exploit this long-range behaviour to obtain a linear-scaling method:
we introduce a spatial cut-off
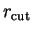 and require that the
density-matrix be strictly zero when the separation of its arguments exceeds
this cut-off;
and require that the
density-matrix be strictly zero when the separation of its arguments exceeds
this cut-off;
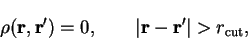 |
(4.68) |
so that the density-matrix now only contains an amount of information
which scales linearly with system-size. Imposing this cut-off naturally
restricts the variational freedom of the density-matrix, so it will be
necessary to converge the ground-state energy with respect to this
parameter in real calculations.
Using the separable form above, we can impose this restriction by requiring
the auxiliary orbitals to be localised in space (i.e. vanishing outside a
certain region of space) and by making the matrix 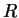 sparse, so that
elements of
sparse, so that
elements of 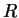 corresponding to orbitals localised in regions separated by
more than the spatial cut-off
corresponding to orbitals localised in regions separated by
more than the spatial cut-off
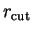 are automatically set to
zero. The localised nature of the auxiliary orbitals requires a localised
basis-set to describe them, and this is the subject of chapter 5.
are automatically set to
zero. The localised nature of the auxiliary orbitals requires a localised
basis-set to describe them, and this is the subject of chapter 5.




Next: 4.6 Non-orthogonal orbitals
Up: 4. Density-Matrix Formulation
Previous: 4.4 Constraints on the
Contents
Peter Haynes
![]() and thus contains an amount of information
which scales as the square of the system-size (as of course it must since
it contains all of the information in the Kohn-Sham orbitals, which are
functions of one position but with the number of occupied orbitals also scaling
linearly with system-size). To obtain a linear-scaling method, it is necessary
to impose some further restrictions on the density-matrix.
and thus contains an amount of information
which scales as the square of the system-size (as of course it must since
it contains all of the information in the Kohn-Sham orbitals, which are
functions of one position but with the number of occupied orbitals also scaling
linearly with system-size). To obtain a linear-scaling method, it is necessary
to impose some further restrictions on the density-matrix.
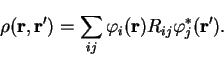
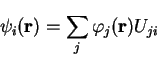
![]() be
the normalised Bloch wave-function for the
be
the normalised Bloch wave-function for the ![]() th band with wave-vector
th band with wave-vector
![]() . Then the corresponding Wannier function for that band
. Then the corresponding Wannier function for that band
![]() is defined by [143]
is defined by [143]
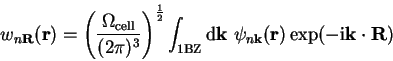
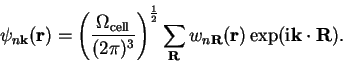
![]() ) and
are orthonormal:
) and
are orthonormal:
![]() -point sampling
-point sampling
![]() is given by
is given by
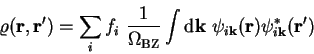
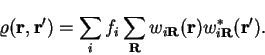
![]() and require that the
density-matrix be strictly zero when the separation of its arguments exceeds
this cut-off;
and require that the
density-matrix be strictly zero when the separation of its arguments exceeds
this cut-off;