



Next: 5. Localised basis-set
Up: 4. Density-Matrix Formulation
Previous: 4.5 Requirements for linear-scaling
Contents
4.6 Non-orthogonal orbitals
We conclude this chapter with a discussion about the representation of the
density-matrix using non-orthogonal orbitals. We consider a set of
non-orthogonal functions
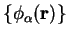 which we denote
which we denote
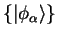 , and introduce their dual functions
defined by
, and introduce their dual functions
defined by
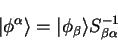 |
(4.69) |
in which the summation convention is assumed and the matrix 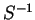 is the
inverse of the overlap matrix
is the
inverse of the overlap matrix 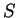 defined by
defined by
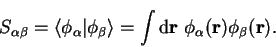 |
(4.70) |
We have assumed from now on that we are only calculating wave-functions at
the 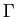 -point and so can assume that everything is real.
By construction, the dual states obey
-point and so can assume that everything is real.
By construction, the dual states obey
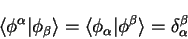 |
(4.71) |
and the completeness relation is expressed as
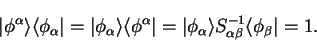 |
(4.72) |
In general we will represent the density-matrix in the separable form
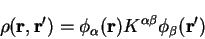 |
(4.73) |
and note that the density-kernel
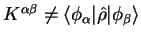 because of the non-orthogonality.
because of the non-orthogonality.
We can construct an orthonormalised set of orbitals
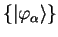 defined as linear combinations of the
defined as linear combinations of the
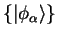 by the
Löwdin transformation:
by the
Löwdin transformation:
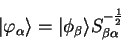 |
(4.74) |
such that
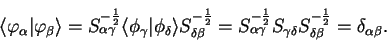 |
(4.75) |
At the ground-state, these orthonormal orbitals
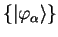 will be a unitary transformation of the Kohn-Sham orbitals
will be a unitary transformation of the Kohn-Sham orbitals
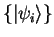 , so that the density-kernel
, so that the density-kernel 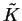 defined as the
density-matrix in the representation of the orthonormalised orbitals
defined as the
density-matrix in the representation of the orthonormalised orbitals
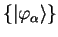 ,
,
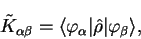 |
(4.76) |
can be diagonalised by a unitary transformation 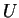 as described in section
4.5.1 i.e.
as described in section
4.5.1 i.e.
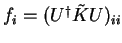 (no summation
convention). The following relationship also holds;
(no summation
convention). The following relationship also holds;
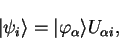 |
(4.77) |
and the relationship between the non-orthogonal orbitals
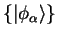 and the Kohn-Sham orbitals
and the Kohn-Sham orbitals
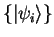 is of the general form
is of the general form
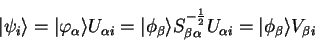 |
(4.78) |
where the matrix
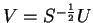 and obeys
and obeys
Using the completeness relation (4.72) we can now express the
matrix 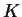 in terms of other quantities:
in terms of other quantities:
so that
In fact, the density-kernel 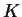 contains the matrix elements of the density-operator
in the representation of the dual vectors of the non-orthogonal functions:
contains the matrix elements of the density-operator
in the representation of the dual vectors of the non-orthogonal functions:
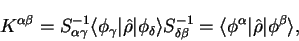 |
(4.84) |
hence the superscript notation.
If we wish to obtain the occupation numbers, we must diagonalise the matrix
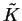 which is given by
which is given by
Thus the eigenvalues of
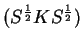 are the occupation
numbers.
are the occupation
numbers.
At the ground-state, the density-operator and Hamiltonian commute, and thus
both the Hamiltonian and the density-matrix can be diagonalised simultaneously.
The Hamiltonian is usually represented by its matrix elements in the
representation of the non-orthogonal orbitals. Thus
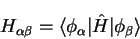 |
(4.86) |
in contrast to the definition of 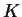 . In this case, to obtain the
eigenvalues of the Hamiltonian
. In this case, to obtain the
eigenvalues of the Hamiltonian
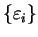 it is necessary to
diagonalise the matrix
it is necessary to
diagonalise the matrix 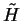
i.e. the eigenvalues of
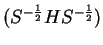 are those
of the Kohn-Sham Hamiltonian.
are those
of the Kohn-Sham Hamiltonian.
The advantage of representing the density-operator and Hamiltonian in
different ways is that quantities such as the electron number and
non-interacting energy can be expressed easily:
since the factors of
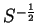 and
and 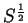 cancel.
cancel.
In the language of tensor analysis, the functions
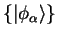 are covariant vectors, and their duals the associated contravariant quantities. The overlap matrix
are covariant vectors, and their duals the associated contravariant quantities. The overlap matrix
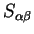 plays the rôle of the metric tensor to convert between covariant and contravariant quantities. This is seen by verifying the relationship
plays the rôle of the metric tensor to convert between covariant and contravariant quantities. This is seen by verifying the relationship
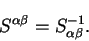 |
(4.90) |
For the orthogonal functions
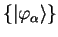 , the metric tensor is the identity and so there is no distinction between covariant and contravariant quantities.
, the metric tensor is the identity and so there is no distinction between covariant and contravariant quantities.
In a linear-scaling scheme we will not be able to access the eigenvalues
directly, since although 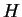 and
and 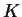 are sparse,
are sparse,
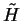 and
and
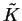 need not be, and in any case, the effort to diagonalise even a
sparse matrix is
need not be, and in any case, the effort to diagonalise even a
sparse matrix is 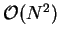 . However it is important to understand the
different origins and rôles of these matrices in order to analyse the
equations which result when we attempt to minimise the total energy to find
the ground-state.
. However it is important to understand the
different origins and rôles of these matrices in order to analyse the
equations which result when we attempt to minimise the total energy to find
the ground-state.




Next: 5. Localised basis-set
Up: 4. Density-Matrix Formulation
Previous: 4.5 Requirements for linear-scaling
Contents
Peter Haynes
![]() which we denote
which we denote
![]() , and introduce their dual functions
defined by
, and introduce their dual functions
defined by
![]() defined as linear combinations of the
defined as linear combinations of the
![]() by the
Löwdin transformation:
by the
Löwdin transformation:
![]() in terms of other quantities:
in terms of other quantities:
![]() which is given by
which is given by
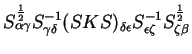
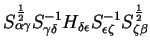
![]() are covariant vectors, and their duals the associated contravariant quantities. The overlap matrix
are covariant vectors, and their duals the associated contravariant quantities. The overlap matrix
![]() plays the rôle of the metric tensor to convert between covariant and contravariant quantities. This is seen by verifying the relationship
plays the rôle of the metric tensor to convert between covariant and contravariant quantities. This is seen by verifying the relationship
![]() and
and ![]() are sparse,
are sparse,
![]() and
and
![]() need not be, and in any case, the effort to diagonalise even a
sparse matrix is
need not be, and in any case, the effort to diagonalise even a
sparse matrix is ![]() . However it is important to understand the
different origins and rôles of these matrices in order to analyse the
equations which result when we attempt to minimise the total energy to find
the ground-state.
. However it is important to understand the
different origins and rôles of these matrices in order to analyse the
equations which result when we attempt to minimise the total energy to find
the ground-state.