Hartree and exchange-correlation energies

The sum of the Hartree and exchange-correlation energies, 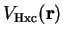$E_{\mathrm {Hxc}}$ depends only on the density so that

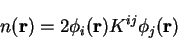$$\frac{\partial E_{\mathrm{Hxc}}}{\partial K^{\alpha \beta}} ... ...f r})} \frac{\partial n({\bf r})}{\partial K^{\alpha \beta}} .$$ (7.23)

The functional derivative of the Hartree-exchange-correlation energy with respect to the electronic density is simply the sum of the Hartree and exchange-correlation potentials, 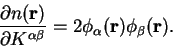$V_{\mathrm{Hxc}}({\bf r})$. The electronic density is given in terms of the density-kernel by

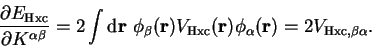$$n({\bf r}) = 2 \phi_i({\bf r}) K^{ij} \phi_j({\bf r})$$ (7.24)

so that we obtain

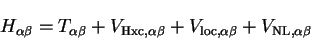$$\frac{\partial n({\bf r})}{\partial K^{\alpha \beta}} = 2 \phi_{\alpha}({\bf r}) \phi_{\beta}({\bf r}) .$$ (7.25)

Finally, therefore

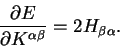$$\frac{\partial E_{\mathrm{Hxc}}}{\partial K^{\alpha \beta}} ... ...r}) \phi_{\alpha}({\bf r}) = 2 V_{\mathrm{Hxc},\beta \alpha} .$$ (7.26)