Total energy

Next: Support function derivatives Up: Density-kernel derivatives Previous: Hartree and exchange-correlation energies Contents

Total energy

Defining the matrix elements of the Kohn-Sham Hamiltonian in the representation of the support functions by

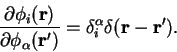$\begin{displaymath} H_{\alpha \beta} = T_{\alpha \beta} + V_{\mathrm{Hxc},\alpha... ... V_{\mathrm{loc},\alpha \beta} + V_{\mathrm {NL},\alpha \beta} \end{displaymath}$

(7.27)

the derivative of the total energy with respect to the density-kernel is simply

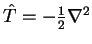$\begin{displaymath} \frac{\partial E}{\partial K^{\alpha \beta}} = 2 H_{\beta \alpha} . \end{displaymath}$

(7.28)

Peter D. Haynes
1999-09-21